
D3D12 内存分配器
D3D12 内存分配器 (D3D12MA) 是一个 C++ 库,它提供了一个简单易集成的 API,可帮助您为 DirectX®12 缓冲区和纹理分配内存。
在计算机图形学中,我们很少遇到连续数据。我们通常处理的是数字数据,而在几何建模的背景下,这意味着我们通常处理多边形网格而不是像 Bézier 曲线那样的过程式曲面。在专用建模软件中创建数字三维对象的最流行技术是多边形建模。创建阶段的结果是一组多边形(网格),其中网格中的多边形可以与其他多边形共享顶点和边。
尽管用户可以创建各种类型的曲面(例如,非流形),但最常见的曲面是拓扑学上的二维流形。简而言之,二维流形是拓扑学中的一个数学概念,其中空间局部看起来像 中的欧几里得平面。本质上,二维流形上的每个点都有一个看起来像平面一部分的邻域。
| 基于三角形的二维流形网格示例 | 基于四边形的二维流形网格示例 |
|
|
在多边形的顶点处,用户可以存储额外的数据(每顶点属性),例如顶点法线(用于模拟曲面)、纹理坐标(用于纹理映射)或 RGBA 颜色。
理论上,可以使用所有类型的多边形。然而,在实践中,3D 图形艺术家最常使用三角形和四边形。这些多边形通常在计算机图形学 API(例如 Microsoft DirectX® 或 Vulkan®)中被称为拓扑图元。从艺术家的角度来看,四边形更具优势,因为它们更容易处理。基于四边形的建模的特性包括:
易于生成网格状曲面。
创建易于调整的边流拓扑(添加或删除边循环时)。
为细分算法产生可预测的结果。
| 不美观的网格 | 美观的网格 |
|
|
这些论点使得四边形拓扑成为艺术家在建模 3D 对象时的首选。
很久以前,GPU 就放弃了对硬件加速的四边形(或包含超过 4 个顶点的多边形)光栅化的支持,因此也放弃了对其顶点中包含的顶点属性的插值(直线渲染是另一回事)。唯一具有硬件加速光栅化和参数插值实现的多边形是三角形。三角形能够胜出是有充分理由的,我只列举几个:
三角剖分定理:该定理指出,由三角形组成的网格可以逼近甚至复杂曲面。
三角形顶点始终位于同一平面上:这是因为任何三个不共线的点在三维空间中总是定义一个平面。
巴里中心坐标:该坐标系在几何学中用于表示点在三角形内的位置。这些坐标可用于在三角形表面上对顶点属性进行插值。
电路复杂性较低:仅支持三角形的光栅化和插值只需要更少的晶体管,这意味着该功能在芯片上占用的空间更少。这可以导致芯片更小(且生产成本更低),或者节省的空间可以用于其他功能。
三角形是实时计算机图形学的基础,这反映在图形 API 支持的图元拓扑中。网格中使用的所有其他多边形类型都必须转换为三角形。当建模应用程序允许四边形网格构建时,该网格的可视化不是基于四边形。相反,应用程序会将它们转换为三角形网格。这种必要的转换会在由凸四边形生成的两个三角形的公共边上,在顶点属性(例如纹理坐标、顶点法线向量和顶点颜色)的插值中引入 不连续性。
就本文的主题而言, 的不连续性是指分段函数连续但其一阶导数不连续的点。换句话说,分段函数本身没有跳跃或中断,但分段函数的斜率(或变化率)有跳跃或中断。
| 连续性 | 不连续性 | |
| 分段函数 |
|
|
| 一阶导数 |
|
|
对于将四边形作为两个三角形进行光栅化,顶点属性插值中的 不连续性在将四边形分割成两个三角形所产生的新边上最为明显。
| 顶点颜色 | 纹理坐标 | 顶点法线 |
 |  |  |
 |  |  |
 |  |  |
本文的目的是提出一种新方法,该方法可以保持由凸四边形生成的两个三角形在公共边上的 连续性。这种新方法基于双线性插值系数代数解,该系数以巴里中心坐标表示。双线性插值在代数角度上是最简单的插值,具有优点。因此,计算开销可忽略不计。此外,线性插值可以轻松构建其他类型的插值,例如多项式插值。然后,将使用 GPU 硬件支持的三种可用硬件加速管线实现并测试该代数解。
目前,解决本文所述问题的努力可以分为以下几种方法:
第一种方法不是消除问题,而是最小化问题。通过将四边形细分,直到渲染伪影变得对观察者不可察觉,或者比光栅化过程中产生的别名伪影更不明显。
可以使用硬件加速的细分着色器阶段在应用程序运行时动态地执行四边形细分。
| 细分级别 1 | 细分级别 2 | 细分级别 3 | 细分级别 4 | 细分级别 5 |
 |  |  |  |  |
或者,可以使用建模软件提供的专用工具(例如 Blender® Subdivision Surface Modifier)在内容创建阶段静态地执行四边形细分。
| 在 Blender 中使用 Subdivision Surface Modifier 之前的网格 | 在 Blender 中使用 Subdivision Surface Modifier 之后的网格 |
|
|
细分网格(无论是在应用程序运行时还是其他时候)都能有效地降低所有类型的 不连续性对观察者的可见度,但代价是降低性能和/或增加网格渲染过程中的内存开销。
在文章 A quadrilateral rendering primitive 中,作者提出了一种硬件加速的四边形光栅化方法,以解决该问题。对于四边形(可能非平面)内部的顶点属性插值,作者选择使用 均值坐标。然而,这些坐标产生的结果与双线性插值类似。可以指出以下几点:
在计算均值坐标时,会使用超越函数。这些函数的值可以通过预定的精度来确定。然而,从性能角度来看,它们会引入一定的开销,具体取决于硬件对超越函数计算的实现。
均值坐标插值不会生成直线,这可能不是用户所期望的。该硬件解决方案在本文撰写时尚未通过 GPU 实现。然而,Barycentric quad rasterization 的作者尝试使用现代 GPU 可用的几何着色器管线来实现它。提出的实现有一个缺点:它使用双精度浮点变量,这会显著影响性能开销。用于实时渲染的 GPU 主要设计用于支持单精度浮点计算。
Inigo Quilez inverse bilinear interpolation – 2010 和 Nathan Reed Quadrilateral Interpolation, Part 2 等作者观察到了双线性插值的优点,并通过使用片段着色器的实现提出了解决方案。
提出的解决方案演示了四边形双线性插值的实现,但它们仅展示了如何为单个四边形及其纹理坐标顶点属性进行插值。它们并未解决如何将其应用于真实三维网格模型的问题。
本文提出的方法包含一个方程,该方程可以用每个凸四边形可以分割成的两个三角形之一的巴里中心坐标 来表示双线性插值系数 。
平面上给定四边形中每一点 的欧几里得坐标可以表示为其顶点的欧几里得坐标的双线性插值。
线段 参数化为 ,
线段 参数化为 ,
线段 参数化为 ,
线段 参数化为 .
点 是线段 和 的交点。
或者,点 的欧几里得坐标可以表示为三角形 ABD \ 的巴里中心坐标:
其中 是正实数,且 。
这可以在二维空间中从几何上证明。
| 四边形内的双线性插值 | 三角形内的重心插值 |
|
|
点的欧几里得坐标无论是在四边形内还是三角形内,都是相同的。
根据点的欧几里得坐标,它可能位于三角形或三角形内。存在一个方程组,使用四边形的顶点和双线性插值系数,以及三角形或的顶点和同一点的重心坐标来描述点的坐标。
点在中的坐标可以通过重心坐标和双线性插值系数和来计算,这些可以通过以下两组独立的方程表示
点在中的坐标可以通过重心坐标和双线性插值系数和来计算,这些可以通过以下两组独立的方程表示
这些方程可以简化为以下形式:
我们可以进一步简化,使用
化为两个方程组
现在,求解关于 和 的两个方程组,这会引出求解两个二次方程的问题。
将此解嵌入到 中,在具有平面法向量 的三角形的表面法向量 平面上,该方程可以写成
其中 是 中的叉积, 是 中的点积。
将三元点积代入方程
最后一步是求解这两个二次方程中关于参数 和 的解。
最后一步是求解这两个二次方程中关于参数 和 的解。
该方程可用于计算三维空间中任意四边形的双线性插值系数 和 。这是因为,如果一个四边形嵌入到 中的任何平面上,都可以通过等距变换将其映射到 平面上,并且等距映射后前提条件仍然成立。
值得注意的是,上述方程表明双线性插值系数 和 取决于四边形顶点 all four Euclidean coordinates。如果是静态网格,这些系数可以预先计算(运行时不需要)。但是,如果是动态(动画)网格,则需要在运行时计算这些系数。因此,我们需要使用一个图形管线阶段,在该阶段我们仍然可以访问四边形顶点的所有四个位置。
当渲染限于平行四边形的四边形时,解决方案要简单得多,因为 。可以从快速分析中推断出这一点。
向量 描述为 . 在平行四边形中,第一个括号内的向量 ,根据定义,其长度与向量 相等,但方向相反。因此,这两个向量的和始终是零向量。
因此,当
这个更简单的案例已经有所描述,解决方案可以在 如何使用现代GPU正确地在平行四边形上插值顶点属性? 中找到。
上一节中提出的代数解决方案的硬件加速实现可以使用三个不同的图形管线阶段来实现:几何着色器、细分着色器和网格着色器。这种三向实现表明,该技术在 2008 年发布的 GPU 硬件上是可行的。以下源代码使用 GLSL 着色语言。
下表描述了实现所提出技术所需的 API 版本和扩展。
| Vulkan® | DirectX® | OpenGL® | |
| 几何着色器 | 启用了 Vulkan® 几何着色器功能 | DirectX® 10 | OpenGL® 3.2 |
| 细分着色器 | 启用了 Vulkan® 细分着色器功能 | DirectX® 11 | OpenGL® 4 |
| 网格着色器 | 启用了 Vulkan® VK_EXT_mesh_shader 扩展 | DirectX® 12 Ultimate | 启用了 OpenGL® 4 GL_NV_mesh_shader 扩展 |
所提出方法实现的实现要求在片段着色器中具有当前处理片段的重心坐标。当以下扩展可用时,这是可能的。
Vulkan® VK_KHR_fragment_shader_barycentric 扩展。
DirectX® 12 Shader Model 6.1。
OpenGL® 4 GL_NV_fragment_shader_barycentric 或 GL_AMD_shader_explicit_vertex_parameter。
如果 GPU 不支持上述扩展,则可以通过几何着色器、细分着色器或网格着色器阶段来生成它们。
本文提出的新方法的实现可以分为以下几个步骤:
将四边形图元传递到图形管线。
现代图形 API(不包括旧的 OpenGL GL_QUADS 和 GL_QUAD_STRIP 图元类型)中不提供四边形图元。为了支持类似四边形的图元,请使用以下方法:
几何着色器:使用几何着色器阶段,邻接图元可用于模拟四边形图元。
OpenGL® GL_LINES_ADJACENCY
Vulkan® VK_PRIMITIVE_TOPOLOGY_LINE_LIST_WITH_ADJACENCY
DirectX® 12/11 D3D_PRIMITIVE_TOPOLOGY_LINELIST_ADJ
通过细分阶段,引入了新的 Patch 图元。在这种拓扑结构中,网格中定义的顶点数量不是固定的,但所谓的控制点每个 Patch 的范围从 1 到 32。这些控制点可以被视为贝塞尔曲面的控制点,但也可以被视为多边形顶点。本文提出的解决方案的实现使用具有 4 个控制点的 Patch,并将其视为四边形的顶点。
网格着色器:使用网格着色器,有多种方法可以将四边形图元引入图形管线。此阶段的开发是为了提供用户更大的灵活性。因此,由用户以某种方式生成包含四边形的网格块(这不属于本文的范围)。
下一步是计算常量 (使用上述步骤之一),然后将其用于片段着色器。我们需要在上述某个管线阶段计算这些常量,因为在片段着色器中,我们无法访问四边形顶点的四个属性(如果存在,重心坐标扩展仅让我们能够访问三角形顶点的三个属性)。通过分析本文方法的代数解,我们可以看到这些常量取决于四边形顶点的位置。
以下函数需要在几何着色器、细分求值着色器或网格着色器中执行。
vec3 calculateConstants(vec3 v0, vec3 v1, vec3 v2, vec3 v3) { const vec3 v10 = v1 - v0; const vec3 v30 = v3 - v0; const vec3 crossv10v30 = cross(v10, v30); const vec3 n = normalize(crossv10v30); const vec3 d = v0 - v1 + v2 - v3; float A_u = dot(n, cross(d, v30)); float A_v = dot(n, cross(d, v10)); const float B = dot(n, crossv10v30); A_u = abs(A_u) < 0.00001 ? 0.0 : A_u; A_v = abs(A_v) < 0.00001 ? 0.0 : A_v; return vec3(A_u, A_v, B); }其中 v0, v1, v2, v3 是按以下顺序排列的四边形顶点的欧几里得坐标。
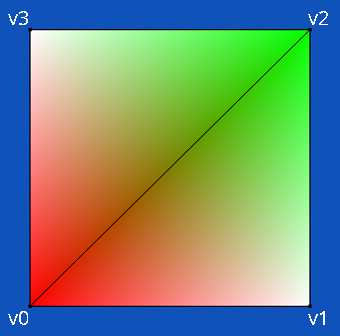
计算出的 A_u, A_v 和 B 值随后传递给片段着色器。
为了使双线性插值在片段着色器中正常工作,我们需要能够在其中获取所有四个顶点属性(例如纹理坐标、顶点法线和顶点颜色)。
layout (location = 0) pervertexEXT in block{ vec3 Normal; flat vec3 NormalExtra; vec2 Texcoord; flat vec2 TexcoordExtra; vec4 Color; flat vec4 ColorExtra; flat vec3 BaryConstants;} In[];layout(location = 0) in block{ flat vec3 Normal[4]; flat vec2 Texcoord[4]; flat vec4 Color[4]; flat vec3 BaryConstants; vec3 BarycentricCoordinate;} In;在使用重心坐标进行顶点属性插值时,它们在三角形中的定义顺序无关紧要。然而,在本文件中所述的实现方法中,特定的顺序很重要。此顺序可以直观地表示如下:
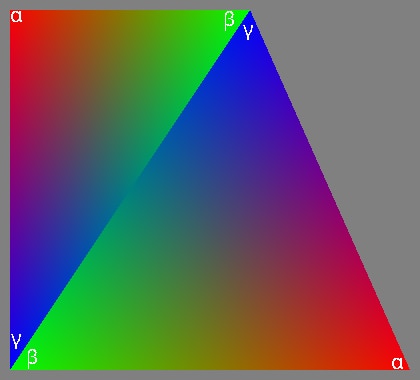
其中 红色 表示 重心坐标的影响,绿色 表示 ,蓝色 表示 。
当存在适当的扩展时,硬件可以提供这种重心坐标顺序,或者可以在细分着色器或几何着色器阶段生成这些数据。
在片段着色器中,可以通过调用以下函数来计算双线性插值系数 和 。
vec2 calculateBilinear(float beta, float gamma, float A_u, float A_v, float B) { const float B_u = B; const float B_v = -B; const float B2 = beta * A_v + gamma * A_u; const float t_u = B_u - B2; const float t_v = B_v - B2; const float b_u = t_u / A_u * 0.5; const float b_v = t_v / A_v * 0.5; const float c_u = gamma * B_v; const float c_v = beta * B_u; const float d_u = b_u * b_u - c_u / A_u; const float d_v = b_v * b_v - c_v / A_v; const float s_u = A_u >= 0.0 ? -1.0 : 1.0; const float s_v = A_v >= 0.0 ? 1.0 : -1.0; const float u = A_u != 0.0 ? (-b_u - s_u * sqrt(d_u)) : (-c_u / t_u); const float v = A_v != 0.0 ? (-b_v - s_v * sqrt(d_v)) : (-c_v / t_v); return vec2(u, v); }其中 beta 是 重心坐标,gamma 是 重心坐标,A_u, A_v, B 是在之前的图形管线阶段计算出的常量。
计算出双线性插值系数 和 后,可以使用函数实现顶点属性的插值。
vec4 interpolateBilinear(vec4 v0, vec4 v1, vec4 v2, vec4 v3, vec2 uv){ return mix(mix(v0, v1, uv.y), mix(v2, v3, uv.y), uv.x);}vec3 interpolateBilinear(vec3 v0, vec3 v1, vec3 v2, vec3 v3, vec2 uv){ return mix(mix(v0, v1, uv.y), mix(v2, v3, uv.y), uv.x);}vec2 interpolateBilinear(vec2 v0, vec2 v1, vec2 v2, vec2 v3, vec2 uv){ return mix(mix(v0, v1, uv.y), mix(v2, v3, uv.y), uv.x);}float interpolateBilinear(float v0, float v1, float v2, float v3, vec2 uv){ return mix(mix(v0, v1, uv.y), mix(v2, v3, uv.y), uv.x);}其中 v0, v1, v2, v3 是四边形顶点属性。
对于仅限于平行四边形的四边形,实现本文所述技术更为简单。
vec4 calculateConstants(vec4 A, vec4 B, vec4 C, vec4 D){ return A - B + C - D;}vec3 calculateConstants(vec3 A, vec3 B, vec3 C, vec3 D){ return A - B + C - D;}vec2 calculateConstants(vec2 A, vec2 B, vec2 C, vec2 D){ return A - B + C - D;}float calculateConstants(float A, float B, float C, float D){ return A - B + C - D;}其中 A, B, C, D 是按规定顺序排列的顶点属性。
每个顶点属性的计算值需要传递给片段着色器。
vec4 interpolateBilinear(vec4 attribute, vec2 barycentric, vec4 extraVal){ return attribute + barycentric.x * barycentric.y * extraVal;}vec3 interpolateBilinear(vec3 attribute, vec2 barycentric, vec3 extraVal){ return attribute + barycentric.x * barycentric.y * extraVal;}vec2 interpolateBilinear(vec2 attribute, vec2 barycentric, vec2 extraVal){ return attribute + barycentric.x * barycentric.y * extraVal;}float interpolateBilinear(float attribute, vec2 barycentric, float extraVal){ return attribute + barycentric.x * barycentric.y * extraVal;}其中 attribute 表示通过传统重心插值(在片段着色器中可用)插值的值,barycentric 是一个 vec2 数据类型,包含片段的 和 重心坐标,extra 是在之前的几何、细分、网格着色器阶段计算出的常量。
本文提出的代数解决方案在不同实现中的输出保持一致。根据顶点属性的类型,结果可以总结在下表中:
| 顶点属性 | 重心插值 | 使用本文提出的解决方案进行双线性插值 |
| 颜色 |  |  |
| 纹理坐标 |  |  |
| 法线 |  |  |
| 颜色 |  |  |
| 纹理坐标 |  |  |
| 法线 |  |  |
| 颜色 |  |  |
| 纹理坐标 |  |  |
| 法线 |  |  |
| 网格示例 |  |  |
| 动画示例 | 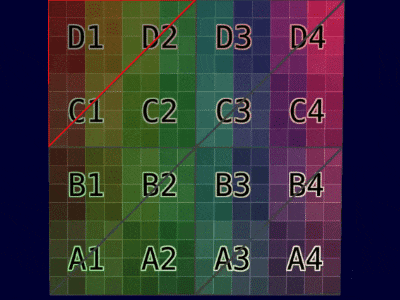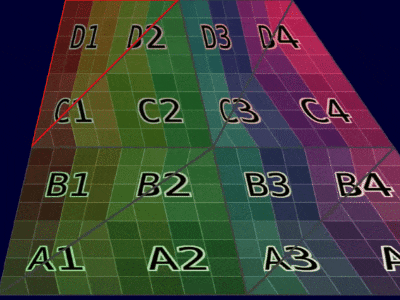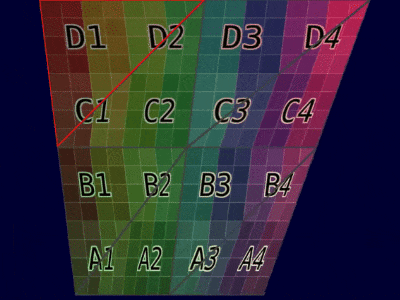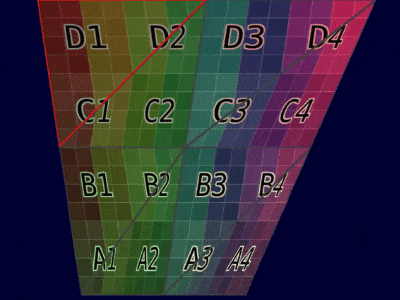 | 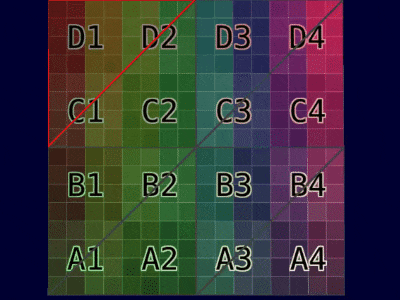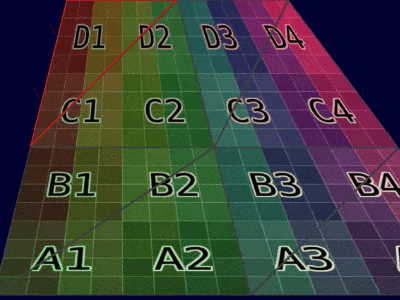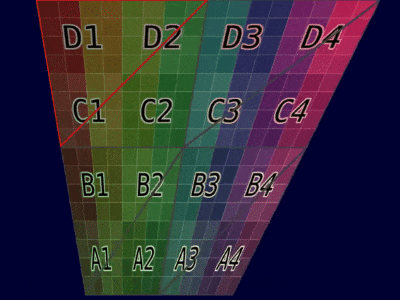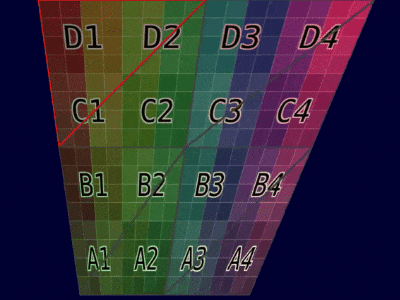 |
如本文所述,使用重心坐标进行双线性插值的代数解决方案可以通过 Vulkan® 或 DirectX® 等 API 来实现。此实现利用 GPU 上的硬件加速渲染。本文提出了三种不同的实现,基于 GPU 支持的可用图形管线。这些实现使得在从 2008 年发布的型号到最新版本的 GPU(包括 PC 和移动设备)上使用新方法成为可能。
Blender 是 Blender Foundation 在欧盟和美国的注册商标。DirectX 是 Microsoft Corporation 在美国和其他司法管辖区的注册商标。OpenGL® 和椭圆形标志是 Hewlett Packard Enterprise 在美国和/或其他国家/地区的商标或注册商标。Vulkan 和 Vulkan 标志是 Khronos Group Inc. 的注册商标。
