الاختيار排序是一种高效的非比较排序算法，可以有效地对整数、字符串甚至浮点数值等离散键进行排序。通常，当排序元素数量很大时，اختيار排序比比较排序算法快得多。它根据键的个位数将键分桶，然后相应地重新排序。由于其稳定性，可以从最低有效位到最高有效位重复此过程。 الاختيار排序也是 GPU 上排序最受欢迎的选择之一，因为它可以通过将输入键分成 GPU 组来利用计算单元并行计算。由于其效率，许多应用程序，如空间数据结构构建，都使用 الاختيار排序。因此，它们可以从优化的排序实现中受益。

通常，GPU اختيار排序可以这样构建：计数键以构建直方图，前缀扫描以计算偏移量，以及重新排序键。当计数和重新排序阶段都从全局内存中多次读取完全相同的值时，就会出现潜在的效率低下，这会产生冗余的内存访问操作。合并内核可以解决冗余问题，但这并不直接。

为了解决这个问题，以前的研究人员提出了Onesweep الاختيار排序算法，通过合并前缀扫描和重新排序阶段来减少全局内存操作的数量，同时通过解耦后视方法最小化延迟。然而，由于 Onesweep 需要一个大小与要排序的元素数量成比例的时间缓冲区，因此在内存分配方面仍有优化的空间。

在本文中，我们介绍了一种在 GPU 上实现的另一种高性能、内存高效的 الاختيار排序实现，它进一步改进了 Onesweep。具体来说，我们提出了一种扩展，通过使用固定大小的循环缓冲区来减少前缀扫描的时间内存分配。我们还介绍了一般优化技术。

传统 الاختيار排序

在深入了解 Onesweep الاختيار排序之前，我们先介绍经典的 الاختيار排序，然后再介绍 Onesweep，因为该算法是从核心概念扩展而来的。اختيار排序算法的过程可以总结为以下三个步骤：计数、前缀扫描和重新排序。在算法开始时，我们计算给定输入数据分区中元素的出现次数，并将结果存储在存储桶中。接下来，为了计算输入数据中每个元素的地址偏移量，我们对上一步的计数结果执行前缀扫描。由于前缀扫描给出了小于某个元素值的总元素计数，因此结果标记了该值的起始偏移量。最后，我们根据计算出的偏移量重新排序给定的输入数据。图 1 概述了排序过程的每次迭代。请注意，计数阶段使用的存储桶大小随着排序的位数而增长。例如，用于计数的 32 位需要 $2^{32}$ 的存储桶大小。然而，由于 الاختيار排序是一种稳定的排序算法，这意味着对于任何两个被认为是等价的元素，经过排序后它们的相对顺序保持不变，我们可以将整个排序过程分成多个传递，并从最低有效位开始，以避免单个巨大的存储桶。

图 1：标准计数-扫描-重排 الاختيار排序每次迭代的概述。此示例演示了 2 位排序。在计数时，为每个数字创建存储桶以记录出现次数。结果传递给前缀扫描，以计算每个数字的全局偏移量。最后，在重排中，这些数字根据计算出的偏移量进行重排并相应地排序。

GPU 上的经典 الاختيار排序

实际上，经典 الاختيار排序的上述三个步骤可以实现为独立的内核在 GPU 上运行。最初，输入元素被分成较小的块并分配给 GPU 块。每个数字和每个 GPU 块的输出偏移量在前缀扫描阶段确定。为了进行并行前缀扫描，要处理的数据（在此示例中，是计数表中存储的元素出现次数）首先被分成块并分配给各个 GPU 块。一种简单但效率低下的实现将需要每个 GPU 块将其部分前缀和输出到全局内存，然后启动另一个内核来合并最终结果。多内核调度会发出全局屏障来同步内核，而部分前缀的传播需要额外的内存传输。因此，这会带来性能损失，因为内核启动和内存传输通常会产生高延迟和开销。

一种优化方法是将前缀扫描计算模式重构为单次内核启动。在此模式下，每个 GPU 块的局部前缀和并行计算，并通过等待前一个块完成局部和来解析每个块的全局偏移量。因此，这种方法有效地将输入 n 个元素的内存访问次数从 3n（读 2n 次，写 n 次）减少到 2n（读 n 次，写 n 次），因为所有计算都可以在单次内核调度中完成。这种方法被称为链式扫描，它是一种解决 GPU 块之间全局偏移量的方法。

经典 الاختيار排序中的一个性能瓶颈是输入被访问两次，一次在计数时，一次在重排时。由于全局内存的访问具有巨大的延迟，并且两次内核之间的读取值相同，因此存在很大的优化空间。此外，链式扫描的性能受到数据传播延迟的阻碍，因为每个 GPU 块都必须等待其直接前驱的前缀和可用。

解耦后视和 Onesweep

在最近的一项开发中，Merrill 等人。引入了一种高效、单次传递的并行前缀扫描计算方法，称为解耦后视，它极大地降低了前缀传播延迟。关键概念是通过让块访问局部和来解耦每个 GPU 块对其直接前驱的单一依赖。解耦后视方法允许 GPU 块通过累积越来越远的局部和来检查前驱的状态。在解耦后视中，前驱中只有一个完成前缀扫描就足以完成后视，而链式扫描方法需要等待直接前驱的前缀扫描完成。

随后，Adinets 和 Merrill 进一步采用了这种概念并将其扩展到所谓的Onesweep算法，这是一种最低有效位 (LSD) الاختيار排序算法，它将分离的内核合并为一个，从而消除了从全局内存多次访问相同输入的需求，从而减少了内存操作的数量。图 2 说明了 Onesweep 中一个特定数字的重排。用于指示块中数字元素的输出位置头部的prefix sum 是通过解耦后视即时计算的。尽管重排内核必须承担解耦后视的成本，但与链式扫描方法相比，GPU 停顿时间非常小。请注意，与经典 الاختيار排序不同，每个数字的输出位置可以提前计算，因为每个数字的全局直方图在排序过程中是不变的。

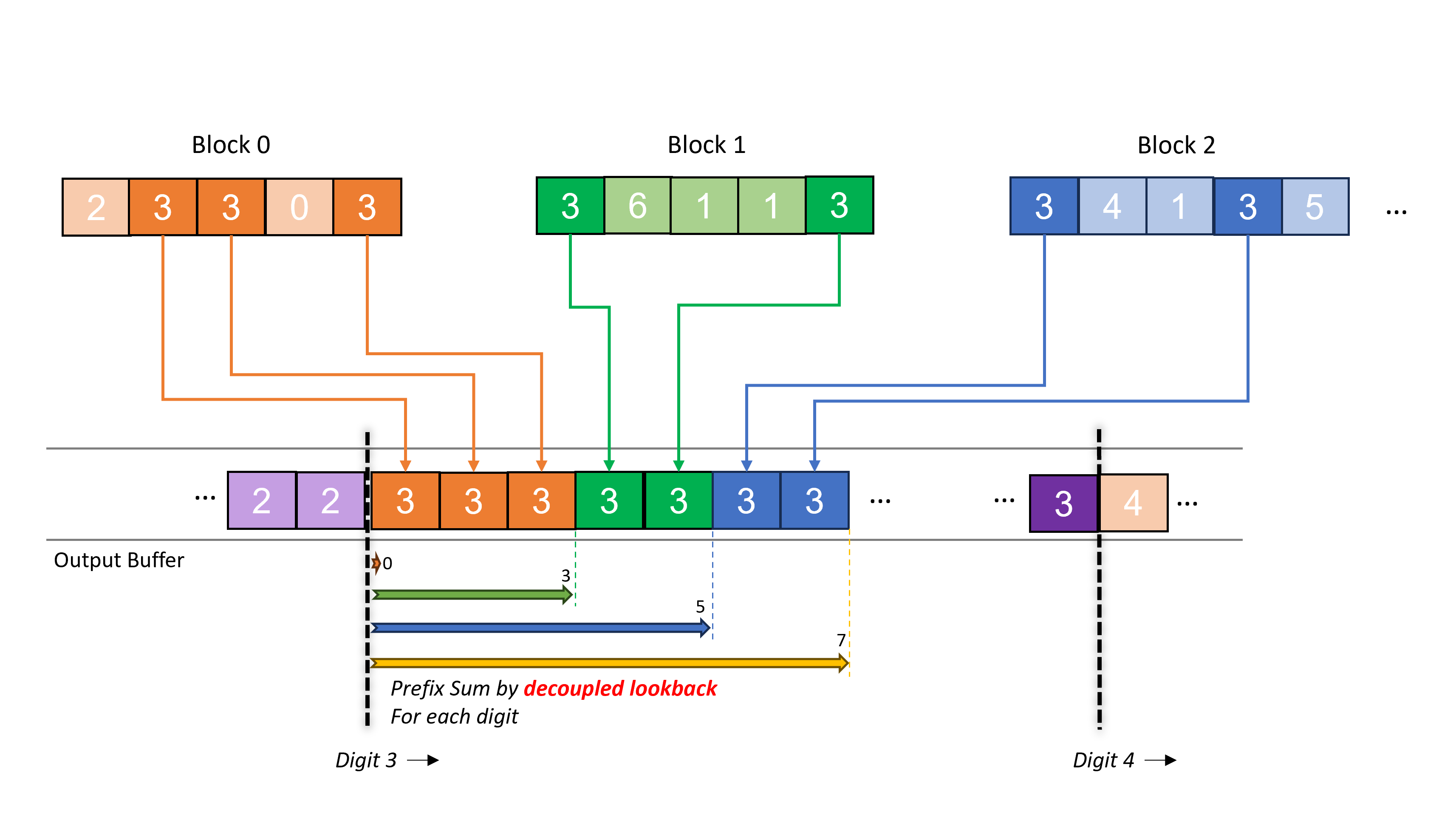图 2：Onesweep 中一个特定数字（此例中为 3）的重排说明。每个块首先为每个数字计算一个局部直方图。通过解耦后视计算每个数字的前缀和，并用于确定全局输出位置。

解耦后视及其实现细节

在解耦后视中，每个 GPU 块都必须公开其局部和及其前缀和，供后续块使用。每个 GPU 块的状态通过块级局部和计算（聚合）来更新。由于每个块的局部和可以独立计算，因此后续块一旦可用就可以自由访问前驱块的局部和。这使得它们能够逐步累积结果，直到达到完整的包含扫描（前缀和）。随后，每个块的状态会根据其前缀和进一步更新。实际上，实现解耦后视需要为每个 GPU 块添加一个额外的状态标志作为变量，指示局部和或前缀和当前是否可用。当一个块观察到其前驱时，它可以简单地引用此状态标志来确定它是否需要累积局部和或使用前缀和并完成该过程。即使直接前驱尚未完成前缀扫描的计算，也可以使用局部和，然后执行将尝试从前驱读取前缀。

图 3 演示了如何执行解耦后视来计算偏移量的前缀和。在图中，每个块的状态转换按时间顺序从上到下显示。虽然在后视过程中无法避免局部和计算本身，但它大大降低了延迟，因为局部和与其他块没有任何依赖关系。

在实际实现中，这个额外的状态标志与局部和和前缀和一起打包在一个 32 位或 64 位结构中。通过位字段定制，该结构的大小设计为与原始类型匹配，确保在更新时将其视为原始类型。这确保了内容（和与标志）在一次指令中被原子地修改。此外，我们使用volatile限定符来确保对该变量的任何引用都编译为实际的内存读写指令。这确保了它的效果对其他 GPU 块立即可见，并且不会被缓存。

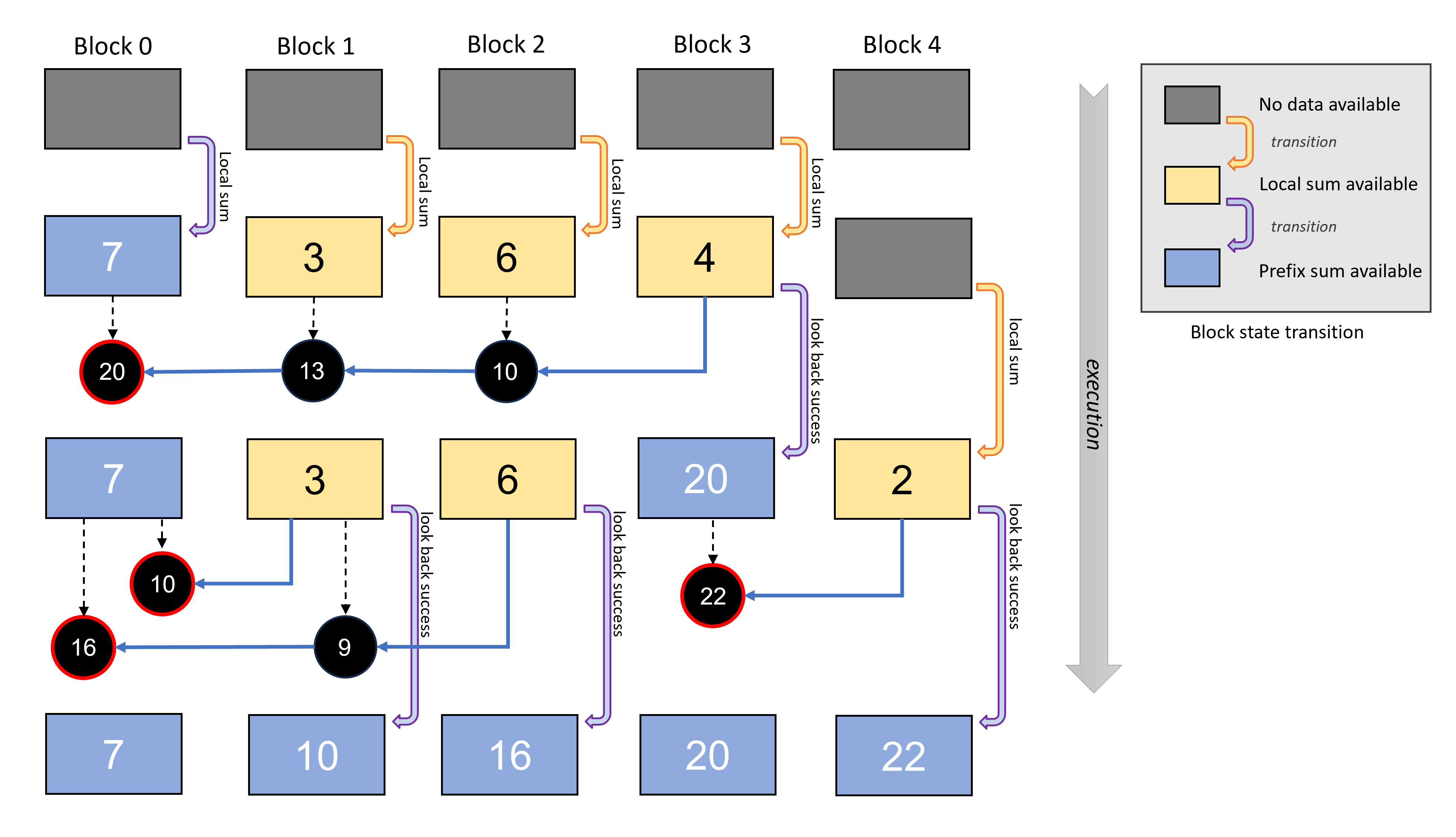图 3：解耦后视过程用于计算前缀和的示例，按时间顺序从上到下。每个块检查索引较低的块，直到前缀和可用（红圈），而无需进行旋转等待。通过这种后视方案，前缀和的计算没有单一依赖性，从而提高了整体效率。

时间内存分配

Onesweep 通过最小化内存带宽、高效执行前缀扫描以及减少内核调度次数来优于传统 الاختيار排序。尽管如此，标准 Onesweep 的一个缺点是它需要时间内存来存储前缀扫描的状态以进行解耦后视，这与要排序的元素数量成比例。这是因为需要维护内存访问局部性和顺序性，从而限制了每个 GPU 块的块大小粒度。因此，我们提出使用循环缓冲区作为时间缓冲区，使分配的大小固定，与输入元素无关。

图 4：循环缓冲区可用于解耦后视。我们使用尾部迭代器来避免覆盖当前正在用于后视的缓冲区。

循环缓冲区

由于标准的解耦后视对于后视没有长度限制，理论上最后一个元素也可以访问第一个元素。这使得缓冲区的重用变得困难。因此，我们将后视的目标元素 L_lookback 的块数限制为使 GPU 块的数据范围可处置。在此约束下，可以保证索引为 [0, i_tail - L_lookback) 的 GPU 块中的数据未被读取，并且可以在循环缓冲区中安全地覆盖，其中 i_tail 是从第一个元素开始连续完成处理的元素的计数。我们称此计数器为尾部迭代器。图 4 显示了尾部迭代器如何定义循环缓冲区上空闲范围的边界。请注意，由于后视可以超出尾部迭代器位置，因此我们可以安全地覆盖的边界偏移 L_lookback。

列表 1 显示了一种通过 GPU 块之间的顺序增量实现的原子操作的朴素尾部迭代器增量实现。这是块的串行执行，导致执行效率低下。因此，我们允许多个块同时运行以增量迭代器。这可以通过允许最低位的乱序增量来缓解停顿。列表 2 是优化后的尾部迭代器实现。由于高位是顺序增量的，因此可以通过丢弃低位来获得尾部迭代器的保守值，其中“保守”是指仍在使用中的 GPU 块的缓冲区区域未被重用。我们利用尾部迭代器来等待前面的 GPU 块，以避免冲突使用循环缓冲区。可以使用循环缓冲区的 GPU 块范围是 [i_tail - L_lookback, i_tail - L_lookback + N_table) ，其中 N_table 是循环缓冲区的大小，因为 [0, i_tail - L_lookback ) 中的数据未被任何 GPU 块读取。我们让解耦后视等待以避免冲突，如列表 3 所示。考虑到后视的长度不能超过循环缓冲区大小，因此 L_lookback 必须小于 N_table。由于 N_table 必须足够大才能利用所有 GPU 处理器，因此 L_lookback < N_table 很容易满足。

// Listing 1: A naïve tail iterator increment.
// The tail iterator is incremented sequentially among GPU blocks in the exact order of the index of the block.


... // Finished the use of the temporal buffer in a block.

__syncthreads();

if( threadIdx.x == 0 )
{
    while( atomicAdd( i_tail, 0 ) != blockIdx.x )
        ;

    atomicInc( i_tail, 0xFFFFFFFF );
}

...

// Listing 2: The optimized tail iterator increment.
// The lower bits of the tail iterator are incremented out of order to reduce spin waiting.

... // Finished the use of the temporal buffer on a decoupled
    // lookback in a block.

__syncthreads();

if( threadIdx.x == 0 )
{
    constexpr u32 TAIL_MASK = 0xFFFFFFFFu << TAIL_BITS;
    while( ( atomicAdd( i_tail, 0 ) & TAIL_MASK ) != ( blockIdx.x & TAIL_MASK ) )
        ;

    atomicInc( i_tail, 0xFFFFFFFF );
}

// Listing 3: A spin-waiting implementation to avoid conflicts of circular buffer use.

if( threadIdx.x == 0 && N_table <= blockIdx.x )
{
    constexpr u32 TAIL_MASK = 0xFFFFFFFFu << TAIL_BITS;
    while( ( atomicAdd( i_tail, 0 ) & TAIL_MASK ) - L_lookback + N_table <= blockIdx.x )
        ;
}
__syncthreads();

... // Decoupled look-back with a circular buffer

... // Increment tail iterator

由于循环缓冲区元素被多个 GPU 块重用，因此每个元素都必须区分它是被需要用于后视的块写入的。因此，我们为表中的每个元素使用一个 64 位变量，除了状态标志外，还包含块索引。尽管这会使分配加倍，并且我们使用一个保守的大数来避免由于循环缓冲区耗尽而导致的旋转等待，但在我们的实现中，循环缓冲区仅分配了 2 MB，这在实践中可以忽略不计。

优化

Onesweep 算法由两个 GPU 内核组成：计数和重排。在本节中，我们将介绍我们在实现中采用的优化技术和策略。

Onesweep 中的计数

我们在单个内核中计算每个数字的全局直方图的前缀和，这样输入元素就只被读取一次。我们将输入分成块，并将直方图计算分配给 GPU 块。由于全局直方图的存储桶大小很小（每个迭代处理 k 位，我们使用 k=8），我们使用共享内存为每个 GPU 块计算直方图的前缀和，并通过 **atomicAdd()** 操作合并它们。我们使用持久线程来最小化 **atomicAdd()** 调用次数。启动的 GPU 块数量是计算出来的，以充分利用 GPU 上的所有处理器。

Onesweep 中的重排

局部排序

GPU 块中的元素被移动到目标位置。由于来自块中连续线程的顺序内存访问被合并为单个事务以降低内存操作成本，因此我们执行每个 GPU 块的局部排序作为一种优化。

并行局部排序

我们使用 GPU 块中的线程执行经典的 الاختيار排序。分配给 GPU 块的元素被进一步分成更小的组，以在 GPU 块中的 warp 之间分配排序工作负载。同一数字的已分配元素的直方图和排序中的局部偏移量很容易在单个线程中计算。但是，由于串行执行模式，我们无法利用 warp 中的所有线程。

结论

在本文中，我们介绍了 الاختيار排序的高级技术。我们首先概述了经典的 الاختيار排序算法，深入探讨了 Onesweep الاختيار排序的细节，然后探讨了我们旨在优化时间内存分配的扩展以及一种特定的后视方案，以使其所需大小与输入元素数量解耦。此外，我们还概述了我们在实现中所采用的一般优化策略。进一步探索优化较小元素数组的排序是一个有趣的未来研究方向。

参考文献

1. 在此处获取示例源代码：Orochi/ParallelPrimitives at main · GPUOpen-LibrariesAndSDKs/Orochi
2. 来自书籍：GPU Zen 3: Advanced Rendering Techniques