使用 HIP RT 光线追踪库加速流体模拟

首次发布：
最后更新：
Tianchen Xu's avatar
作者：Tianchen Xu
Takahiro Harada's avatar
原田孝裕 (Takahiro Harada)

引言

HIP RT 是一个主要用于加速光线追踪应用程序的光线追踪库。然而，由于该库的通用性，它也可用于不同领域的应用程序。在本博文中，我们将介绍 HIP RT 在物理模拟中的一个有趣应用。具体来说，我们展示了如何使用 HIP RT 来加速平滑粒子流体动力学 (SPH) 模拟 [1] 中的邻域搜索。虽然加速粒子流体模拟在 GPU 上的研究由来已久 [2]，但正如您从这篇博文中了解到的，HIP RT 使在 GPU 上实现 SPH 模拟变得容易。

在不考虑不可压缩性的基本 SPH 实现方面，计算成本最高的过程是粒子邻域搜索。在各种用于邻域搜索的数据结构中，存在结构化和非结构化组织。均匀网格是一种典型的结构化组织，它将模拟空间划分为均匀的单元格。这也表明模拟空间受限于网格的范围，因为它为网格定义的整个空间分配了内存。与此同时，包围盒层次结构 (BVH) 是一种非结构化组织。虽然在 BVH 上的搜索通常不如使用均匀网格快 [3]，但使用 BVH 的优势在于我们无需限制模拟空间。因此，对于大规模场景，它能够提供更好的灵活性，并为稀疏分布的粒子节省内存空间。

在这里，我们开始看到这两个应用程序之间的一些共同点，即空间加速数据结构 BVH。大多数光线追踪实现都使用 BVH 方案，例如 DirectX 和 Vulkan 光线追踪 (DXR 和 Vulkan RT)。根据 DXR 和 Vulkan RT 规范 [4, 5]，仅当相交光线长度 t 值满足 Tmin<t<TmaxT_\text{min} \lt t \lt T_{max}时才能发生光线与三角形的相交。光线与程序化图元的相交，只有当相交 t 值满足 Tmin≤t≤TmaxT_\text{min} \leq t \leq T_\text{max}时才能发生。HIP RT 也采用了相同的规则。因此，如果我们改变光线为一个零长度光线，我们就可以用它来查找点与轴对齐包围盒 (AABB) 的交集，这正是我们在粒子流体模拟中需要执行的操作。找到邻近粒子后，我们需要从它们计算一些物理量，这可以通过自定义相交函数来实现，HIP RT 也提供了该函数。因此，我们拥有了使用 HIP RT 实现 SPH 模拟所需的所有组件。

关于 SPH 流体模拟

平滑粒子流体动力学 (SPH) 是一种基于粒子的流体模拟方法，与欧拉网格方法相对，也称为拉格朗日方法。它关注受其他粒子影响的每个粒子的动态属性，例如密度、力（或加速度）、速度和位置。对于每个粒子 ii，在位置 ri\mathbf{r}_i 处，其属性量 AiA_i 通过以下模型 [6] 以核密度估计 (KDE) 的形式（所有粒子的贡献的加权和）进行插值：

Ai(ri)=∑jmjAjρjW(ri−rj,h)(1)A_i(\mathbf{r}_i) = \sum_j m_j \dfrac{A_j}{\rho_j}W\left(\mathbf{r}_i - \mathbf{r}_j, h\right) \tag{1}

其中 jj 遍历所有粒子，mjm_j 是粒子 jj 的质量，rjr_j 是其位置，ρj\rho_j 是密度，AjA_j 是粒子 jj 对应的属性量。函数 W(r,h)W(\mathbf{r},h) 称为平滑核，其核半径为 hh。

根据基本 SPH 模型，模拟过程可以分为三个计算通道，每个通道都是一个粒子遍历过程。

首先，对于每个粒子，我们遍历半径 hh 内的所有邻近粒子，获取它们的位置，计算粒子距离，并使用下面的 KDE 公式评估粒子密度值 ρi\rho_i，其中 W=Wpoly6W = W_\text{poly6}：

ρi(ri)=∑jmjρjρjW(ri−rj,h)=∑j∥ri−rj∥≤hmjWpoly6(ri−rj,h)(2)\rho_i(\mathbf{r}_i) = \sum_j m_j \dfrac{\rho_j}{\rho_j}W\left(\mathbf{r}_i - \mathbf{r}_j, h\right) = \sum_j^{\|\mathbf{r}_i - \mathbf{r}_j\| \leq h} m_j W_\text{poly6}\left(\mathbf{r}_i - \mathbf{r}_j, h\right) \tag{2}j∑∥ri​−rj​∥≤h​mj​Wpoly6​(ri​−rj​,h)(2) Wpoly6(r,h)={31564πh9(h2−r2)30≤∥r∥≤h0otherwise(3)W_\text{poly6}(\mathbf{r}, h) = \begin{cases} \dfrac{315}{64\pi h^9}\left(h^2 - \mathbf{r}^2\right)^3 & 0 \leq \|\mathbf{r}\| \leq h\\ 0 & \text{otherwise} \end{cases} \tag{3}

其次，对于每个粒子，我们遍历半径hh内的所有近邻粒子，获取它们的rr、压力pp和速度，并分别使用WspikyW_\text{spiky}和WviscosityW_\text{viscosity}计算压力和粘度项的加速度贡献。

fipressure(ri)=−∑j∥ri−rj∥≤hmjpi+pj2ρj∇Wspiky(ri−rj,h)(4)\mathbf{f}_i^\text{pressure}(\mathbf{r}_i) = -\sum_j^{\|\mathbf{r}_i - \mathbf{r}_j\| \leq h} m_j \dfrac{p_i + p_j}{2\rho_j} \nabla W_\text{spiky}\left(\mathbf{r}_i - \mathbf{r}_j, h\right) \tag{4} ∇2Wviscosity(r,h)={45πh6(h−∥r∥)0≤∥r∥≤h0otherwise(7)\nabla^2 W_\text{viscosity}(\mathbf{r}, h) = \begin{cases} \dfrac{45}{\pi h^6}\left(h - \|\mathbf{r}\|\right) & 0 \leq \|\mathbf{r}\| \leq h\\ 0 & \text{otherwise} \end{cases} \tag{7}

其中，pip_i和pjp_j 分别表示粒子ii和jj的压力值。压力值pp可以根据密度值由p=k((ρρ0)3−1)p = k\left(\left(\frac{\rho}{\rho_0}\right)^3 - 1\right)推导得出，其中kk是取决于温度的气体常数，ρ0\rho_0是静止密度。

fiviscosity(ri)=μ∑j∥ri−rj∥≤hmjvj−viρj∇2Wviscosity(ri−rj,h)(6)\mathbf{f}_i^\text{viscosity}(\mathbf{r}_i) = \mu\sum_j^{\|\mathbf{r}_i - \mathbf{r}_j\| \leq h} m_j \dfrac{\mathbf{v}_j - \mathbf{v}_i}{\rho_j} \nabla^2 W_\text{viscosity}\left(\mathbf{r}_i - \mathbf{r}_j, h\right) \tag{6}

其中，vi\mathbf{v}_i和vj\mathbf{v}_j 分别表示粒子ii和jj的速度值，μ\mu为粘度系数。

最后，对于每个粒子，我们计算内部（压力和扩散）及外部力的合力，并根据 Navier-Stokes 方程更新加速度、速度和位置：

∂v∂t+v⋅∇v=−∇pρ+μρ∇2v+fexternal=fpressure+fviscosity+fexternal(8)\dfrac{\partial\mathbf{v}}{\partial t} + \mathbf{v}\cdot\nabla\mathbf{v} = -\dfrac{\nabla p}{\rho} + \dfrac{\mu}{\rho}\nabla^2\mathbf{v} + \mathbf{f}^\text{external} = \mathbf{f}^\text{pressure} + \mathbf{f}^\text{viscosity} + \mathbf{f}^\text{external} \tag{8}

其中，fexternal\mathbf{f}^\text{external}是外部力的加速度贡献。这里，符号f\mathbf{f}在许多计算机图形学论文中习惯上被用作表示力，但实际上是加速度值。

如上一节所述，密度和力计算的主要两个处理过程是根据公式（1）的模式实现的。对于每个粒子，我们需要通过迭代邻域搜索来收集核心半径hh内近邻粒子的属性。对于每次搜索迭代，我们查找hh内的粒子并访问其属性数据。这个过程成本很高，实现一个快速优化的邻域搜索算法并非易事。幸运的是，通过利用 hiprtGeomCustomTraversalAnyHit，我们可以方便地迭代访问指定影响半径hh内的所有粒子属性。

首先，我们以公式（2）为例，使用 HIP RT 实现密度核程序。

extern "C" __global__ void
DensityKernel( hiprtGeometry geom, float* densities, const Particle* particles, Simulation* sim, hiprtFuncTable table )
{
    const unsigned int idx      = blockIdx.x * blockDim.x + threadIdx.x;
    Particle           particle = particles[idx];


    hiprtRay ray;
    ray.origin    = particle.Pos;
    ray.direction = { 0.0f, 0.0f, 1.0f };
    ray.minT      = 0.0f;
    ray.maxT      = 0.0f;


    hiprtGeomCustomTraversalAnyHit tr( geom, ray, hiprtTraversalHintDefault, sim, table );


    float rho = 0.0f;
    while ( tr.getCurrentState() != hiprtTraversalStateFinished )
    {
        hiprtHit hit = tr.getNextHit();
        if ( !hit.hasHit() ) continue;


        rho += calculateDensity( hit.t, sim->m_smoothRadius, sim->m_densityCoef );
    }


    densities[idx] = rho;
}

在密度核函数程序中，densities 是一个输出缓冲区，particles 是一个输入粒子数据缓冲区（包括粒子位置和速度），而 sim 是一个包含模拟参数的常量缓冲区。在这里，我们首先将 hiprtRay 设置为一个零长度的射线，方向任意且已归一化，其 ray.minT = ray.maxT = 0。然后，我们以交互方式访问命中结果，直到任何命中状态为 hiprtTraversalStateFinished。为了安全起见，我们显式跳过了未命中迭代。对于每次迭代，我们按照公式 (2, 3) 调用 calculateDensity 来计算密度。

__device__ float calculateDensity( float r2, float h, float densityCoef )
{
  // Implements this equation:
  // W_poly6(r, h) = 315 / (64 * pi * h^9) * (h^2 - r^2)^3
  // densityCoef = particleMass * 315.0f / (64.0f * pi * h^9)
  const float d2 = h * h - r2;


  return densityCoef * d2 * d2 * d2;
}

对于 hiprtGeomCustomTraversalAnyHit，我们还需要设计一个自定义的相交函数，该函数存储在 hiprtFuncTable 中，并由 getNextHit 隐式调用。

__device__ bool intersectParticleImpactSphere( const hiprtRay& ray, const void* data, void* payload, hiprtHit& hit )
{
    float3      from     = ray.origin;
    Particle    particle = reinterpret_cast<const Particle*>( data )[hit.primID];
    Simulation* sim      = reinterpret_cast<Simulation*>( payload );
    float3      center   = particle.Pos;
    float       h        = sim->m_smoothRadius;


    float3 d  = center - from;
    float  r2 = dot( d, d );
    if ( r2 >= h * h ) return false;


    hit.t      = r2;
    hit.normal = d;


    return true;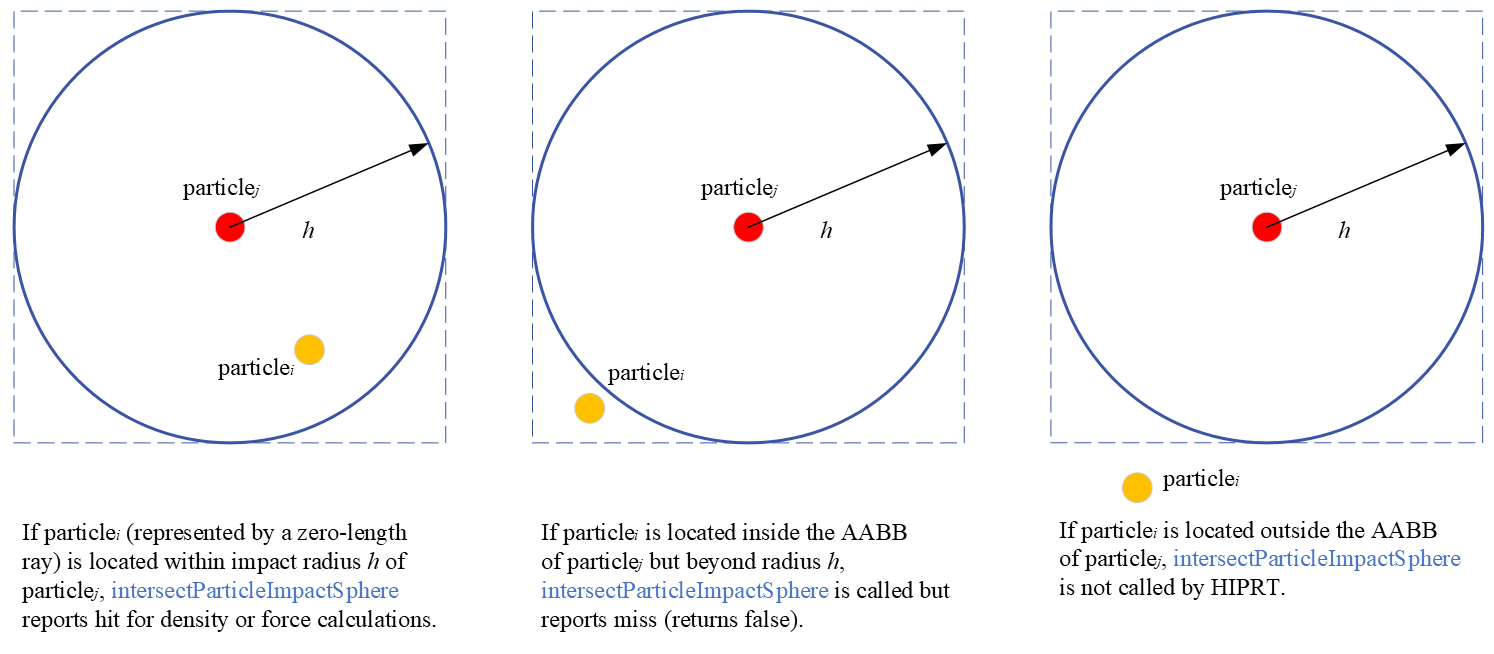
}

在 intersectParticleImpactSphere 中，我们获取射线起点作为粒子 的位置，以及粒子 的位置。然后，通过球形检查，剔除超出碰撞半径 的粒子。接着，我们利用 t（当前射线长度）和 normal 插槽，分别将平方距离 r2 和位移向量 d 的值存储到命中对象中，并将它们传递给主核函数程序。这些值将用于后续的密度和力计算。

对于第二次模拟迭代，我们有一个类似的核函数程序用于力评估。

extern "C" __global__ void ForceKernel(
  hiprtGeometry  geom,
  float3*         accelerations,
  const Particle* particles,
  const float*  densities,
  Simulation*     sim,
  hiprtFuncTable  table )
{
  const unsigned int idx      = blockIdx.x * blockDim.x + threadIdx.x;
  Particle           particle = particles[idx];
  float              rho      = densities[idx];


  hiprtRay ray;
  ray.origin    = particle.Pos;
  ray.direction = { 0.0f, 0.0f, 1.0f };
  ray.minT      = 0.0f;
  ray.maxT      = 0.0f;


  float pressure = calculatePressure( rho, sim->m_restDensity, sim->m_pressureStiffness );


  hiprtGeomCustomTraversalAnyHit tr( geom, ray, hiprtTraversalHintDefault, sim, table );


  float3 force = make_float3( 0.0f );
  while ( tr.getCurrentState() != hiprtTraversalStateFinished )
  {
    hiprtHit hit = tr.getNextHit();
    if ( !hit.hasHit() ) continue;
    if ( hit.primID == idx ) continue;


    Particle hitParticle = particles[hit.primID];
    float   hitRho      = densities[hit.primID];


    float3 disp        = hit.normal;
    float  r           = sqrtf( hit.t );
    float  d           = sim->m_smoothRadius - r;
    float  hitPressure = calculatePressure( hitRho, sim->m_restDensity, sim->m_pressureStiffness );


    force += calculateGradPressure( r, d, pressure, hitPressure, hitRho, disp, sim->m_pressureGradCoef );
    force += calculateVelocityLaplace( d, particle.Velocity, hitParticle.Velocity, hitRho, sim->m_viscosityLaplaceCoef );
  }


  accelerations[idx] = rho > 0.0f ? force / rho : make_float3( 0.0f );
}

ForceKernel 用于评估粒子 由于内部力产生的加速度贡献，其代码模式与 DensityKernel 相同。在这里，为了避免冗余的数据访问和计算以优化性能，当 = 时，我们跳过了对粒子 命中的计算。此外，我们使用与密度核相同的自定义相交函数。另外，基于公式 (4-7) 计算压力、压力梯度和粘性项的函数实现如下。

__device__ float calculatePressure( float rho, float rho0, float pressureStiffness )
{
  // Implements this equation:
  // Pressure = B * ((rho / rho_0)^3 - 1)
  const float rhoRatio = rho / rho0;


  return pressureStiffness * max( rhoRatio * rhoRatio * rhoRatio - 1.0f, 0.0f );
}


__device__ float3
calculateGradPressure( float r, float d, float pressure, float pressure_j, float rho_j, float3 disp, float pressureGradCoef )
{
  float avgPressure = 0.5 * ( pressure + pressure_j );
  // Implements this equation:
  // W_spiky(r, h) = 15 / (pi * h^6) * (h - r)^3
  // GRAD(W_spiky(r, h)) = -45 / (pi * h^6) * (h - r)^2
  // pressureGradCoef = particleMass * -45.0f / (pi * h^6)


  return pressureGradCoef * avgPressure * d * d * disp / ( rho_j * r );
}


__device__ float3
calculateVelocityLaplace( float d, float3 velocity, float3 velocity_j, float rho_j, float viscosityLaplaceCoef )
{
  float3 velDisp = ( velocity_j - velocity );
  // Implements this equation:
  // W_viscosity(r, h) = 15 / (2 * pi * h^3) * (-r^3 / (2 * h^3) + r^2 / h^2 + h / (2 * r) - 1)
  // LAPLACIAN(W_viscosity(r, h)) = 45 / (pi * h^6) * (h - r)
  // viscosityLaplaceCoef = particleMass * viscosity * 45.0f / (pi * h^6)


  return viscosityLaplaceCoef * d * velDisp / rho_j;
}

对于最后的模拟迭代，我们组合了一个积分核函数程序，用于计算每个粒子内部力和外部力的合力，并根据公式 (8) 更新加速度、速度、位置和 AABB。

extern "C" __global__ void IntegrationKernel(
  Particle* particles, Aabb* particleAabbs, const float3* accelerations, const Simulation* sim, const PerFrame* perFrame )
{
  const unsigned int idx          = blockIdx.x * blockDim.x + threadIdx.x;
  Particle           particle     = particles[idx];
  float3             acceleration = accelerations[idx];


  // Apply the forces from the map walls
  for ( u32 i = 0; i < 6; ++i )
  {
    float d       = dot( make_float4( particle.Pos, 1.0f ), sim->m_planes[i] );
    acceleration += min( d, 0.0f ) * -sim->m_wallStiffness * make_float3( sim->m_planes[i] );
  }


  // Apply gravity
  acceleration      += perFrame->m_gravity;


  // Integrate
  particle.Velocity += perFrame->m_timeStep * acceleration;
  particle.Pos      += perFrame->m_timeStep * particle.Velocity;


  Aabb aabb;
  aabb.m_min = particle.Pos - sim->m_smoothRadius;
  aabb.m_max = particle.Pos + sim->m_smoothRadius;


  // Update
  particles[idx]     = particle;
  particleAabbs[idx] = aabb;
}

基于上一次迭代计算出的内部力加速度值，我们部署了一个简单的边界条件模型，该模型根据墙面和刚度参数 m_wallStiffness 反映粒子从撞击墙面时的运动，并将反射累积作为加速度值的外部力贡献。此外，我们还需要添加重力贡献。利用这个合加速度，我们可以轻松地依次推导出新的速度、位置和 AABB 值。

基于主机的实现，使用 HIP RT。

首先，我们定义了两个结构体来表示缓冲区 Simulation 和 Particle，用于存储必要的输入参数和粒子数据。

struct Simulation
{
    float  m_smoothRadius;
    float  m_pressureStiffness;
    float  m_restDensity;
    float  m_densityCoef;
    float  m_pressureGradCoef;
    float  m_viscosityLaplaceCoef;
    float  m_wallStiffness;
    u32    m_particleCount;
    float4 m_planes[6];
};


struct Particle
{
    float3 Pos;
    float3 Velocity;
};

我们为如下描述的场景填充了这两个缓冲区的初始数据。

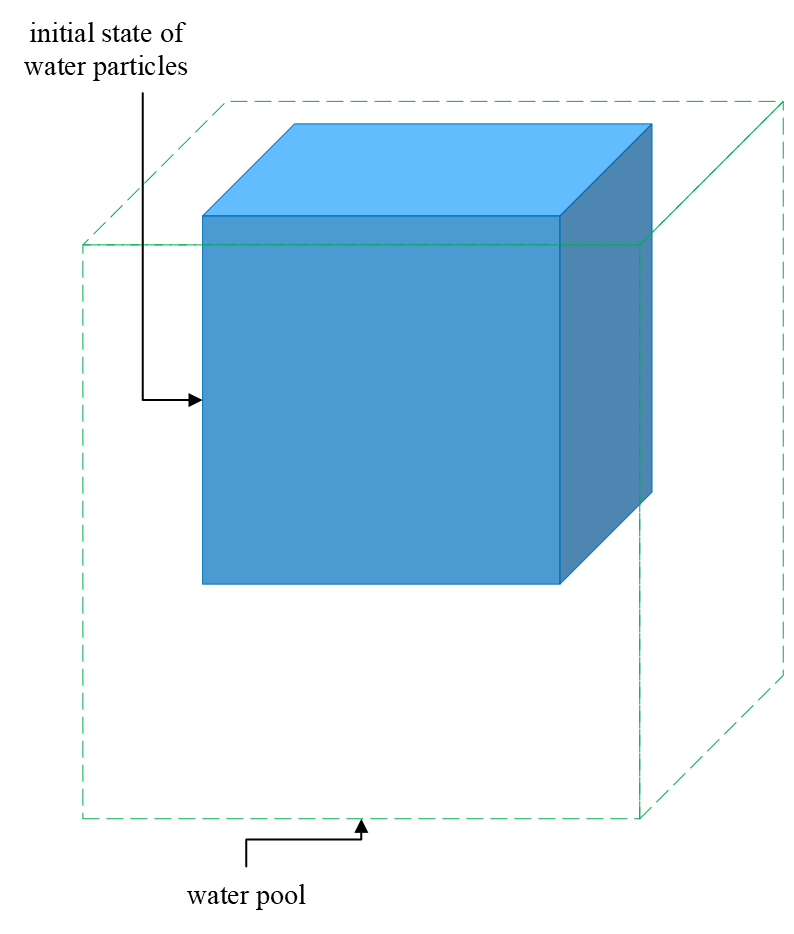
在一个 1 m³ 的立方形水池中，水粒子从水池顶部落下。水的初始体积为一个 0.216 m³ 的立方体。水粒子均匀分布在水体积中，粒子数量为 131,072。其他参数请参考水的属性，例如静止密度 1000 kg/m³，以及根据上述条件推导出的粒子质量。粘度值为 0.4。所有水池壁面的刚度值为 3000。粒子搜索半径指定为 0.02 m，即 SPH 平滑半径 。

接下来，射线追踪的一个非常重要的步骤是构建一个加速结构（AS）。在这里，为了方便起见，我们选择 hiprtGeometry，它只包含底层 AS。我们将 hiprtPrimitiveTypeAABBList 作为相应的 hiprtGeometryBuildInput 的类型。对于每个 AABB 元素，我们根据初始粒子位置填充初始数据。

hiprtAABBListPrimitive list;
list.aabbCount  = sim.m_particleCount;
list.aabbStride = sizeof( Aabb );
std::vector<Aabb> aabbs( sim.m_particleCount );
for ( u32 i = 0; i < sim.m_particleCount; ++i )
{
    const hiprtFloat3& c = particles[i].Pos;
    aabbs[i].m_min.x     = c.x - smoothRadius;
    aabbs[i].m_max.x     = c.x + smoothRadius;
    aabbs[i].m_min.y     = c.y - smoothRadius;
    aabbs[i].m_max.y     = c.y + smoothRadius;
    aabbs[i].m_min.z     = c.z - smoothRadius;
    aabbs[i].m_max.z     = c.z + smoothRadius;
}

由于粒子 AABB 可以每帧更新，我们选择 hiprtBuildFlagBitPreferFastBuild 模式来构建加速结构，并将每帧重建整个 hiprtGeometry。

hiprtGeometryBuildInput geomInput;
geomInput.type               = hiprtPrimitiveTypeAABBList;
geomInput.aabbList.primitive = list;
geomInput.geomType           = 0;


size_t            geomTempSize;
hiprtDevicePtr    geomTemp;
hiprtBuildOptions options;
options.buildFlags = hiprtBuildFlagBitPreferFastBuild;
CHECK_HIPRT( hiprtGetGeometryBuildTemporaryBufferSize( ctxt, geomInput, options, geomTempSize ) );
CHECK_ORO( oroMalloc( reinterpret_cast<oroDeviceptr*>( &geomTemp ), geomTempSize ) );


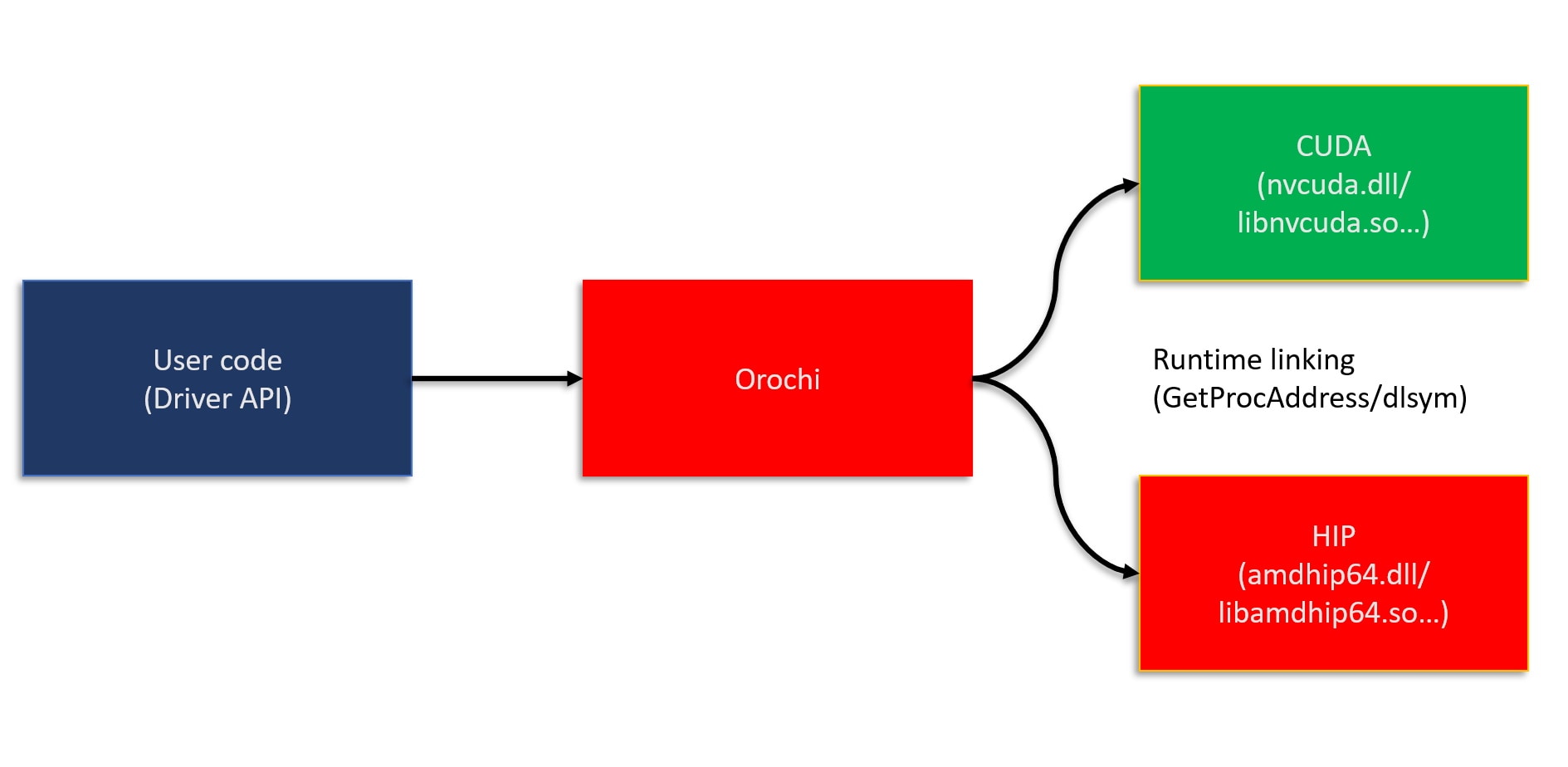
hiprtGeometry geom;
CHECK_HIPRT( hiprtCreateGeometry( ctxt, geomInput, options, geom ) );

在这里，您可以看到 oro 函数，这些函数是 Orochi 库 的函数，该库封装了 HIP 和 CUDA API。因此，使用 Orochi 编写的代码也可以在非 AMD GPU 上运行。

然后，我们为自定义相交函数注册了函数表。如前所述，我们对密度核函数程序和力核函数程序都使用了相同的相交函数 intersectParticleImpactSphere。

hiprtFuncNameSet funcNameSet;
funcNameSet.intersectFuncName              = "intersectParticleImpactSphere";
std::vector<hiprtFuncNameSet> funcNameSets = { funcNameSet };


hiprtFuncDataSet funcDataSet;
CHECK_ORO( oroMalloc(
    reinterpret_cast<oroDeviceptr*>( &funcDataSet.intersectFuncData ),
    sim.m_particleCount * sizeof( Particle ) ) );
CHECK_ORO( oroMemcpyHtoD(
    reinterpret_cast<oroDeviceptr>( funcDataSet.intersectFuncData ),
    particles.data(),
    sim.m_particleCount * sizeof( Particle ) ) );


hiprtFuncTable funcTable;
CHECK_HIPRT( hiprtCreateFuncTable( ctxt, 1, 1, funcTable ) );
CHECK_HIPRT( hiprtSetFuncTable( ctxt, funcTable, 0, 0, funcDataSet ) );

设置函数表后，我们可以相应地构建三个模拟迭代的核函数程序。同时，我们也分配了每个迭代的相应输出缓冲区。

// Density
float*      densities;
oroFunction densityFunc;
CHECK_ORO( oroMalloc( reinterpret_cast<oroDeviceptr*>( &densities ), sim.m_particleCount * sizeof( float ) ) );
buildTraceKernelFromBitcode(
    ctxt, "../common/TutorialKernels.h", "DensityKernel", densityFunc, nullptr, &funcNameSets, 1, 1 );


// Force
hiprtFloat3* accelerations;
oroFunction  forceFunc;
CHECK_ORO(
    oroMalloc( reinterpret_cast<oroDeviceptr*>( &accelerations ), sim.m_particleCount * sizeof( hiprtFloat3 ) ) );
buildTraceKernelFromBitcode(
    ctxt, "../common/TutorialKernels.h", "ForceKernel", forceFunc, nullptr, &funcNameSets, 1, 1 );


// Integration
PerFrame*  pPerFrame;
oroFunction intFunc;
{
    PerFrame perFrame;
    perFrame.m_timeStep = 1.0f / 320.0f;
    perFrame.m_gravity  = { 0.0f, -9.8f, 0.0f };
    CHECK_ORO( oroMalloc( reinterpret_cast<oroDeviceptr*>( &pPerFrame ), sizeof( PerFrame ) ) );
    CHECK_ORO( oroMemcpyHtoD( reinterpret_cast<oroDeviceptr>( pPerFrame ), &perFrame, sizeof( PerFrame ) ) );
    buildTraceKernelFromBitcode( ctxt, "../common/TutorialKernels.h", "IntegrationKernel", intFunc );
}

最后，我们可以构建一个主模拟循环来按顺序分派 HIP RT 核函数。对于每一帧的迭代，我们首先重建 HIP RT 几何以更新 AS，然后启动核函数程序，并将所需缓冲区的指针放入核函数的入口参数中。

const u32 b   = 64; // Thread block size
u32       nb = ( sim.m_particleCount + b - 1 ) / b; // Number of blocks


// ...


// Simulate
for ( u32 i = 0; i < FrameCount; ++i )
{
    CHECK_HIPRT( hiprtBuildGeometry( ctxt, hiprtBuildOperationBuild, geomInput, options, geomTemp, 0, geom ) );


    void* dArgs[] = { &geom, &densities, &funcDataSet.intersectFuncData, &pSim, &funcTable };
    CHECK_ORO( oroModuleLaunchKernel( densityFunc, nb, 1, 1, b, 1, 1, 0, 0, dArgs, 0 ) );


    void* fArgs[] = { &geom, &accelerations, &funcDataSet.intersectFuncData, &densities, &pSim, &funcTable };
    CHECK_ORO( oroModuleLaunchKernel( forceFunc, nb, 1, 1, b, 1, 1, 0, 0, fArgs, 0 ) );


    void* iArgs[] = { &funcDataSet.intersectFuncData, &list.aabbs, &accelerations, &pSim, &pPerFrame };
    CHECK_ORO( oroModuleLaunchKernel( intFunc, nb, 1, 1, b, 1, 1, 0, 0, iArgs, 0 ) );


    // ...
}

结论

HIP RT 具有与 DXR 和 Vulkan RT 类似的功能，它提供了一种更简单、更灵活的替代方案来实现流体模拟中使用的点查询进行邻域搜索，方法是利用快速动态几何体加速结构更新和自定义相交函数。邻域搜索的 BVH 遍历可以由 HIP RT 高效地自动隐式完成。我们最近发布了新版本的 HIP RT (v.2.1)，其中添加了更多功能。我们很乐意听取您关于 HIP RT 的有趣用例。

此示例已包含在 HIP RT SDK 教程中 (https://github.com/GPUOpen-LibrariesAndSDKs/HIPRTSDK)。

参考文献

  1. R. A. Gingold, J. J. Monaghan, Smoothed particle hydrodynamics: theory and application to non-spherical stars, Monthly Notices of the Royal Astronomical Society, Volume 181, Issue 3, December 1977, Pages 375–389, https://doi.org/10.1093/mnras/181.3.375
  2. Takahiro Harada; Seiichi Koshizuka; Yoichiro Kawaguchi (2007). Smoothed particle hydrodynamics on GPUs. Computer Graphics International. pp. 63–70。
  3. Tianchen Xu; Wen Wu; Enhua Wu (2014). Real-time generation of smoothed-particle hydrodynamics-based special effects in character animation. Computer Animations and Virtual Worlds, 25: 185–198。
  4. DirectX Raytracing (DXR) Functional Spec, https://msdocs.cn/DirectX-Specs/d3d/Raytracing.html
  5. Vulkan 1.3 specification, https://registry.khronos.org/vulkan/specs/1.3/html/
  6. Matthias Müller, David Charypar, and Markus Gross. 2003. Particle-based fluid simulation for interactive applications. In Proceedings of the 2003 ACM SIGGRAPH/Eurographics symposium on Computer animation (SCA ‘03). Eurographics Association, Goslar, DEU, 154–159, https://matthias-research.github.io/pages/publications/sca03.pdf
Tianchen Xu's avatar

作者：Tianchen Xu

Tianchen Xu 是 AMD 上海 Khronos3D 团队的研究员和技术支持（MTS）软件开发工程师。
Takahiro Harada's avatar

原田孝裕 (Takahiro Harada)

Takahiro Harada 是 AMD 的一名研究员，也是一款名为 Radeon ProRender 的 GPU 全局照明渲染器的架构师。

相关软件

相关新闻和技术文章

AMD GPUOpen
隐私 商标 供应链透明度 条款和条件 Cookie 政策

©2025 Advanced Micro Devices, Inc.

© . This site is unofficial and not affiliated with AMD.