Matrix Compendium 简介

首次发布：
最后更新：

矩阵汇编

引言

本文的主要目标是将计算机图形学中的变换知识整合到一个单一的、全面的资源中。
尽管这些概念在线上广泛可用，但它们通常以零散的片段呈现，缺乏对其细微之处的连贯解释。本文旨在弥补这些不足，并提供对该主题的透彻理解。

许多现实世界的问题乍一看似乎很简单，但仔细检查后会发现其潜在的复杂性。为了全面探讨这些挑战，我们将采用著名的**分而治之**技术。通过将这个复杂的问题分解成更小的子问题并逐个解决，我们可以创建一个结构化的参考指南。
这种方法将为计算机图形学中变换中经常遇到的挑战带来清晰和条理。

这些子问题可以从数学（理论）和实现（实践）的角度进行分类，如下所示：

  • 矩阵乘法的顺序：确保操作遵循一致的排序规则。

  • 三维欧几里得空间的手性：确定方向约定，例如右手定则。

  • 笛卡尔坐标系中基向量的顺序：确定定义轴的顺序。

  • 将矩阵存储在内存中作为多维数组：优化内存表示以实现高效计算。

矩阵 101

在本文中，我们将深入探讨矩阵及其属性。在深入了解细节之前，让我们简要回顾一些对于理解其细微差别至关重要的基础概念。

什么是矩阵？

在数学中，矩阵本质上是组织成行和列的数字的矩形数组。
例如，下面的矩阵有**3 行**和**5 列**，可以称为一个3×5\mathbf{3 \times 5} 矩阵

[m11m12m13m14m15m21m22m23m24m25m31m32m33m34m35]\begin{array}{c} \begin{bmatrix} m_{11} & m_{12} & m_{13} & m_{14} & m_{15}\\ m_{21} & m_{22} & m_{23} & m_{24} & m_{25}\\ m_{31} & m_{32} & m_{33} & m_{34} & m_{35}\\ \end{bmatrix} \end{array}

为什么矩阵对计算机图形很重要？

答案可以总结为以下几点：

  • 它们作为一种出色的代数工具，以结构化的方式表示几何图形。

  • 三维欧几里得空间中的变换，如仿射变换和投影变换，可以使用4×4\mathbf{4 \times 4} 矩阵来表示。

  • 变换的连接，或两个变换的组合，可以用矩阵乘法来表示。

  • 行或列只有一个的矩阵（换句话说，行向量或列向量）可以存储网格顶点。

  • 将网格顶点从一个空间变换到另一个空间，再次使用了矩阵乘法。

  • 矩阵本身以及对矩阵进行的操作可以在计算机图形应用程序中高效实现。

如何计算矩阵乘法？

矩阵乘法的算法不像矩阵加法那样直接，在矩阵加法中，两个矩阵的对应元素逐个相加。相反，它稍微复杂一些，涉及到通过一系列操作组合行和列。
为了说明这个概念，请考虑以下可视化：

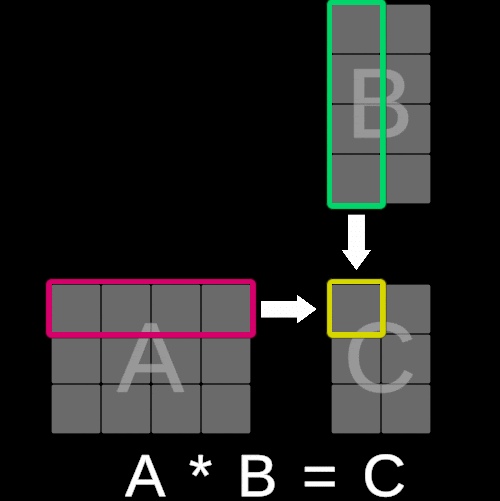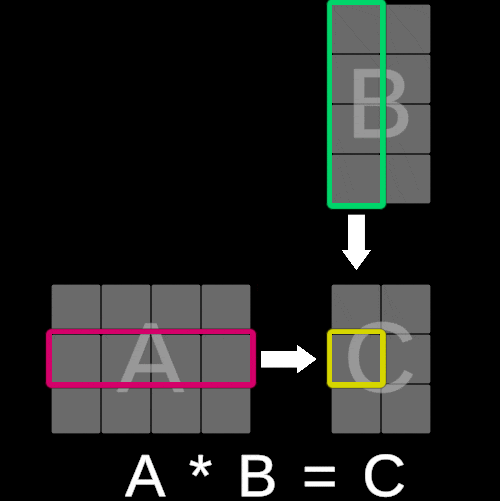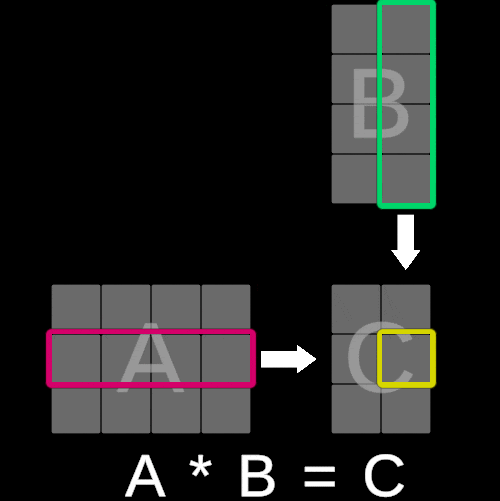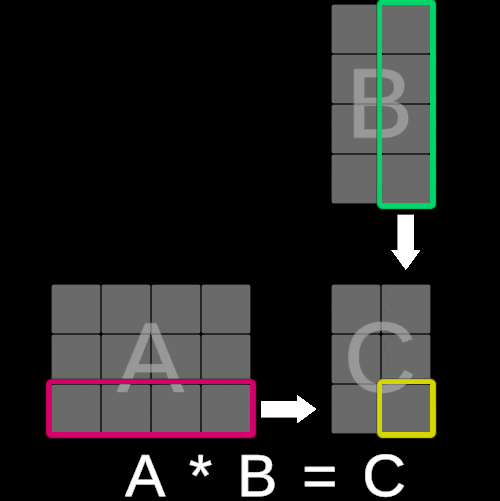
_images/mult_anim.gif

矩阵 C 中每个元素的值是通过将矩阵 A 的第 i 行的每个对应项与矩阵 B 的第 j 列相乘并对这些乘积求和来计算的。本质上，这个操作等同于执行矩阵 A 的第 i 行与矩阵 B 的第 j 列之间的**点积**。

请注意：

  1. 矩阵乘法通常**不可交换**——乘法中乘数的顺序很重要。

  2. 要使矩阵乘法有效，第一个矩阵（运算符左侧）的**列数**必须等于第二个矩阵（运算符右侧）的**行数**。

[a11a12a21a22a31a32a41a42]∗[b11b12b13b21b22b23]=[c11c12c13c21c22c23c31c32c33c41c42c43]\begin{array}{c} \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \\ a_{41} & a_{42} \\ \end{bmatrix} * \begin{bmatrix} b_{11} & b_{12} & b_{13}\\ b_{21} & b_{22} & b_{23}\\ \end{bmatrix} = \begin{bmatrix} c_{11} & c_{12} & c_{13}\\ c_{21} & c_{22} & c_{23}\\ c_{31} & c_{32} & c_{33}\\ c_{41} & c_{42} & c_{43}\\ \end{bmatrix} \end{array}

相关软件

相关新闻和技术文章

相关视频

© . This site is unofficial and not affiliated with AMD.