使用 Mesh Shaders 进行字体和矢量艺术渲染

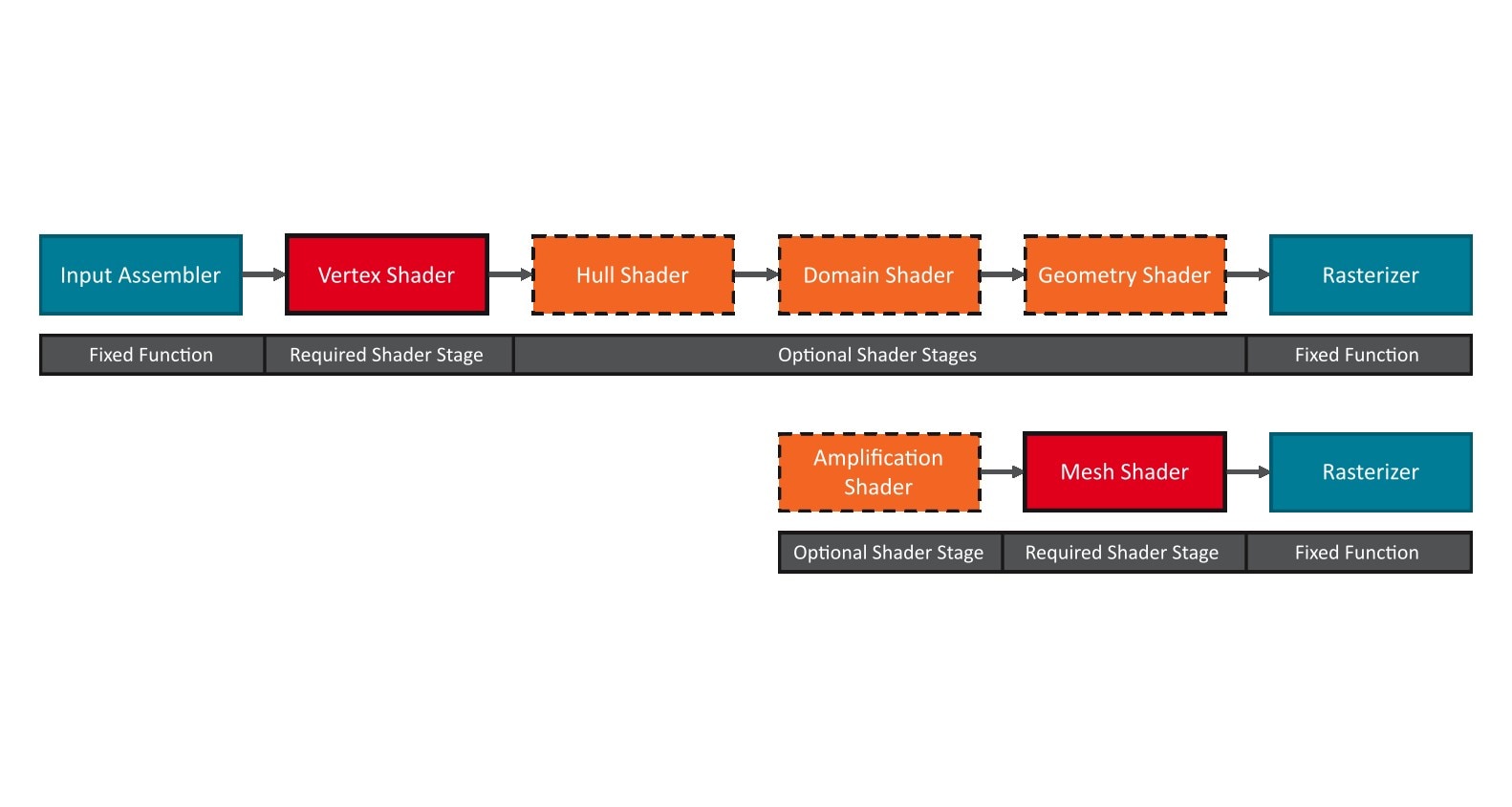
在之前的博文中，我们向您介绍了从顶点着色器到网格着色器的转变。此外，我们还展示了如何测量和优化性能以及最佳实践。

在这篇博文中，我们演示了每图元属性以及如何使用它们来简化字体渲染。每图元属性是通过网格着色器引入的。使用我们在此处使用的字体渲染技术，我们仅通过每个字符串一次绘制调用即可获得无限级别的细节，但这仅在使用网格着色器时可行。我们发现这是一个不错、足够简单、实用且有用的示例，用于探索网格着色器带来的新功能。

缩放	调试视图

引言

字体渲染可能是最普遍的计算机图形学问题之一。事实上，您现在正在阅读的这篇博文，如果没有字体渲染，您将无法阅读。由于其无处不在，我们认为字体渲染是理所当然的，但很少承认其挑战，甚至不欣赏其算法。

字体由字形组成。字形是字符的图形表示，例如字母、数字、符号等。字体渲染是将字形字符串绘制到光栅显示器上的过程。

在这篇博文中，我们展示了如何使用网格着色器来实现 Loop 和 Blinn 在 2005 年 SIGGRAPH 会议论文“使用可编程图形硬件进行分辨率无关的曲线渲染”中的方法。

然而，他们最初的顶点着色器管线实现存在三个缺点：

1. 顶点重复，即共享曲线字形的控制点。这导致不必要的冗余。
2. 该方法需要三种不同的图元类型，这使得每个字形最多需要三次绘制调用。
3. 渲染字符串涉及大量的 API 开销，因为我们必须为每个字符发出最多三次绘制调用。这会导致效率低下，尤其是对于只包含少量三角形的字形。

作为改进，我们做出了以下贡献：

1. 为了消除顶点重复，我们建议使用光栅化阶段提供的重心坐标。然而，这不是网格着色器附带的功能。事实上，它已经存在一段时间了，但它使我们的网格着色器实现更简单。
2. 我们通过网格着色器引入的每图元属性来避免多余的绘制调用。有效地，一个字形可以使用单个顶点和索引缓冲区加上一个新颖的每图元属性缓冲区来表示。有了这个额外的每图元属性缓冲区，一次分派就足以渲染一个字形。
3. 通过我们的网格着色器实现，我们所要做的就是将您要渲染的字符串上传到 GPU 缓冲区。然后一次网格着色器分派即可渲染整个字符串。

我们此处提出的方法也适用于矢量图。然而，关于性能和性能优化的比较案例研究超出了这篇博文的范围。这篇博文应主要关注网格着色器提供的每图元属性功能，并通过实际示例进行演示，也许还能为您提供一些灵感。

字形表示

我们从 TrueType 字体格式 (TTF) 获取字体。在那里，字形由两种类型的曲线组成：线性曲线，它们实际上是线段，以及二次曲线。我们使用线性曲线来绘制“L”之类的字母中的直线边缘，二次曲线用于模拟“.”（句号/点/全句号）之类的字符中的圆形形状，而“S”之类的字母则包含线性曲线和二次曲线的混合。在图中，我们用紫罗兰色笔触突出显示线段，用橙色笔触突出显示二次曲线。线段的端点用黑点标记。

线条	曲线	线条与曲线

多条曲线被组织起来形成一个闭合连续样条，即曲线的有序序列。相邻的曲线在一个共同点相遇。这就是为什么样条称为连续。此外，第一条和最后一条曲线也需要相邻。然后，样条形成一个循环。这就是为什么我们将样条称为闭合。上面的字形“L”、“.”和“S”就是其中一个字形只包含一个闭合连续样条的例子。

一个字形可能包含多个样条，例如分号“;”由两个样条组成。样条甚至可以嵌套形成像“O”这样的字符。

两个独立的样条	两个嵌套的样条

为了确定一个点是否需要填充，我们从该点发射一条射线到一个任意方向。如果该射线与样条相交偶数次，那么我们就位于填充部分的外部。

根据 Loop 和 Blinn 的方法进行字体渲染

TTF 使用贝塞尔曲线表示线性和二次曲线段：对于线性曲线段，公式为

$\vec{f}(t) = (1-t)\cdot\vec{a} + t\cdot\vec{b},\quad t\in\left[0\dots 1\right]$

以及二次贝塞尔曲线段

$\vec{f}(t) = (1-t)^2\cdot\vec{a} + 2(1-t) t \cdot \vec{c}+t^2\cdot\vec{b},\quad t\in\left[0\dots 1\right],$

其中 $\vec{a}$, $\vec{c}$，以及 $\vec{b}$ 是控制点。非字母顺序并非笔误：这样做是为了在两种情况下，$\vec{a}$ 和 $\vec{b}$ 是曲线段的端点。

Loop and Blinn 渲染两种类型的曲线，但二次曲线更有趣。考虑右括号字形 “)”

它由四个二次曲线段组成，其控制点为 $\left(\vec{a}_0,\vec{c}_0,\vec{b}_0\right)$, $\left(\vec{a}_1,\vec{c}_1,\vec{b}_1\right)$, $\left(\vec{a}_3,\vec{c}_3,\vec{b}_3\right)$，以及 $\left(\vec{a}_4,\vec{c}_4,\vec{b}_4\right)$，以及 $\left(\vec{a}_2,\vec{b}_2\right)$ 和 $\left(\vec{a}_5,\vec{b}_5\right)$。它还有两个线性段：$\left(\vec{a}_2,\vec{b}_2\right)$ 和 $\left(\vec{a}_5,\vec{b}_5\right)$。

为了得到字形的一个“有棱角的”近似，我们计算点集 $\left\lbrace\vec{a}_i, \vec{b}_i, \vec{c}_i\right\rbrace$ 在以下约束条件下

• 保持边 $\left(\vec{a}_i, \vec{b}_i\right)$，如果二次曲线是凸轮廓，或者曲线是线性的；
• 保持边 $\left(\vec{a}_i, \vec{c}_i\right)$, $\left(\vec{c}_i, \vec{b}_i\right)$，如果二次曲线是凹轮廓。

在我们的括号示例中，$\left(\vec{a}_0,\vec{c}_0,\vec{b}_0\right)$，$\left(\vec{a}_1,\vec{c}_1,\vec{b}_1\right)$，$\left(\vec{a}_3,\vec{c}_3,\vec{b}_3\right)$，$\left(\vec{a}_4,\vec{c}_4,\vec{b}_4\right)$ 都是凸的，而 $\left(\vec{a}_1,\vec{c}_1,\vec{b}_1\right)$ 都是凹的。这里展示了一个示例细分

我们称“有棱角的近似”的三角形为实心三角形。然而，字形仍然显得有棱角。为了得到平滑的轮廓，我们需要添加下方所示的二次贝塞尔曲线，蓝色表示凸形，红色表示凹形。

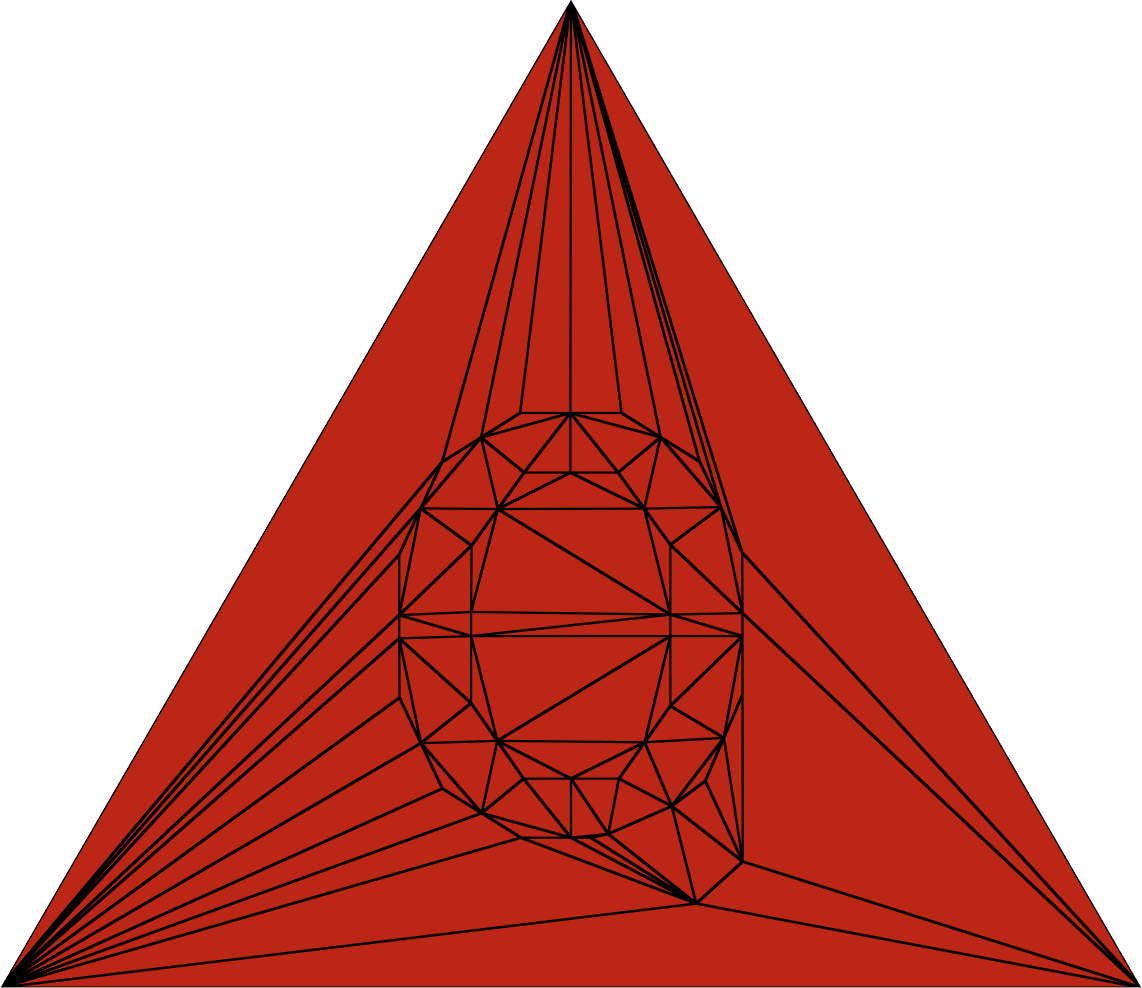
在详细介绍如何渲染贝塞尔曲线之前，让我们快速概述一下如何找到实心三角形。在那里，我们使用许多开源包中的一个，它们会生成所谓的约束 Delaunay 三角剖分。它们通常会进行标准的凸 Delaunay 三角剖分（左侧），可以移除外部三角形（中间），甚至可以检测孔洞（右侧）。我们使用后者来处理字体。

带有外部三角形	不带外部三角形，但填充了孔洞	带有外部三角形并移除孔洞

我们可以使用传统的顶点着色器管线，将结果渲染为具有索引和顶点缓冲区的常规三角形网格。

现在，我们已经完成了实心三角形部分。接下来，我们必须处理构成二次贝塞尔曲线的三角形（即前面蓝色和红色的三角形）。

要渲染二次贝塞尔曲线，Loop and Blinn 建议渲染一个三角形，如下所示

• 每个顶点编码
  • 二次贝塞尔曲线的顶点位置：控制点 $\vec{a}$, $\vec{c}$, $\vec{b}$ 的二次贝塞尔曲线和
  • 2D坐标 $\vec{u}$：2D标准二次贝塞尔曲线 $\vec{u}^{(a)}=\left[0;0\right]^\top$, $\vec{u}^{(c)}=\left[\frac{1}{2};0\right]^\top$, and $\vec{u}^{(b)}=\left[1;1\right]^\top$, and
• 取决于我们想要凸曲线还是凹曲线，像素着色器会丢弃那些插值 $\vec{u}=[u,v]^\top$ 的像素 $u^2-v$ 的值是
• $u^2-v > 0$ 或
• $u^2-v < 0$，分别。

这通过丢弃贝塞尔曲线三角形一侧的像素来渲染二次贝塞尔曲线。由此产生的填充区域形成凸形或凹形区域。

凸形	凹形

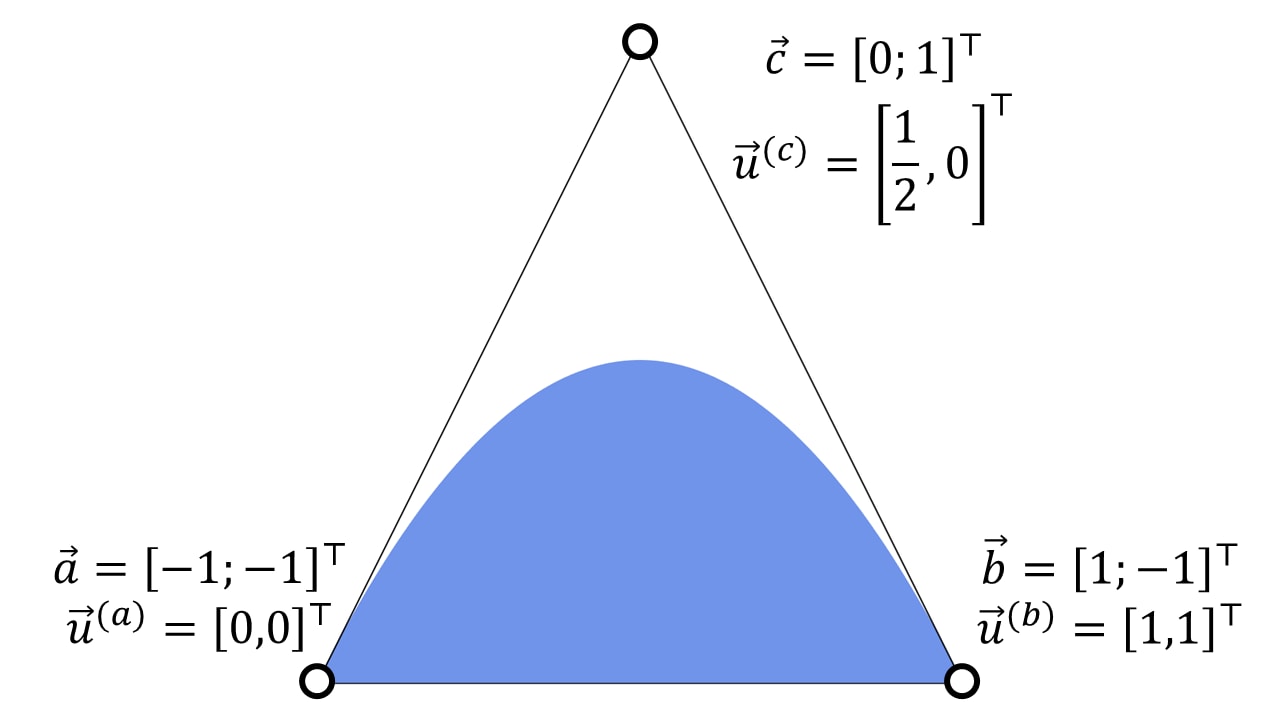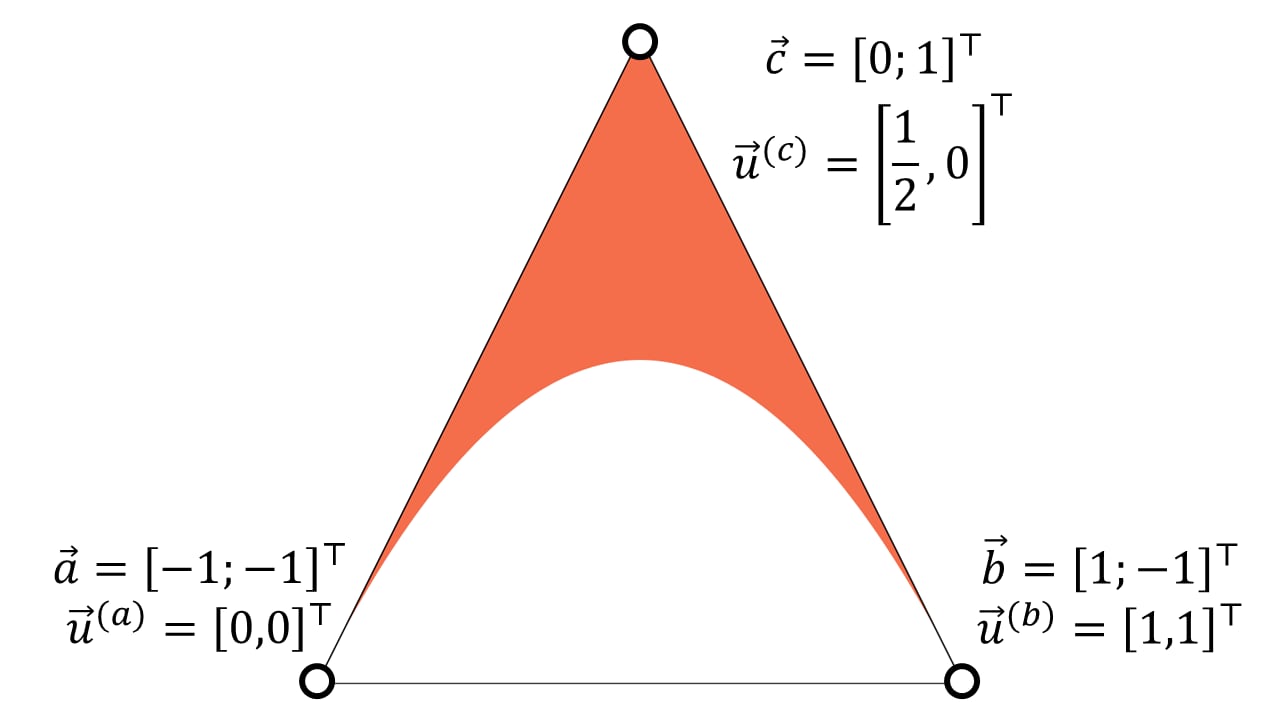以下是此方法有效的原因：查看标准二次贝塞尔曲线的坐标，我们得到