程序化草渲染

首次发布：2024年3月20日

Carsten Faber

Bastian Kuth

Quirin Meyer

Max Oberberger

引言

精细的植被在提高电子游戏的沉浸感方面起着重要作用。植被的一部分就是草。在这篇博文中，我们希望利用网格着色器在 GPU 上生成草丛。为此，我们从 Jahrmann 和 Wimmer 2017 年的 i3D 论文《面向通用 3D 场景的响应式实时草渲染》中汲取灵感，他们利用细分着色器来细分预定义的草叶。这样做的好处是可以生成额外的细节，而无需显式存储它们。我们进一步发展了这一概念，使用一个网格着色器线程组来渲染一整片草丛。虽然在这篇文章中，我们创建了一个风格化的草甸以保持简单，但我们相信我们的技术可以应用于更逼真的场景。

从一根草到一片草甸

这篇博文的结构如下：首先，我们将解释用于表示一根草的参数以及我们如何使用贝塞尔曲线来表示我们的草。接下来，我们将计算顶点、它们的法线和从贝塞尔曲线表示的草叶派生的图元，并说明草叶如何组合成草丛。然后，我们将解释如何高效地将索引和顶点写入 GPU。接下来，我们将概述如何在远处减少几何体数量，同时保持外观一致，并解释我们如何模拟风对草甸的影响。我们将描述我们的像素着色器如何用于改善草的外观，最后，我们将提供一些关于我们的工作如何扩展和改进的建议。

生长一根草

每根草都有一个位置 bladePosition、方向 bladeDirection 和高度 bladeHeight。我们使用这些来计算二次贝塞尔曲线的控制点 $P_0$ , $P_1$ and $P_2$ to represent the shape of a blade of grass.

const static float grassLeaning = 0.3f;
float3 p0 = bladePosition;
float3 p1 = p0 + float3(0, 0, bladeHeight);
float3 p2 = p1 + bladeDirection * bladeHeight * grassLeaning;

$P_0$ is simply bladePosition. $P_1$ is $P_0$ translated upwards by bladeHeight $h$ . To obtain $P_2$ , we translate $P_1$ by the bladeDirection vector $\vec{d}$ scaled with bladeHeight times a leaning factor of grassLeaning = $0.3$ . This preserves the shape of the blade of grass, regardless of its bladeHeight.

Control points side view

To animate the grass we move $P_2$ , which modifies the length of the Bézier curve. To preserve the length of the curve, we use a function to modify $P_1$ and $P_2$ to retain the length of the curve, using the function from Jahrmann and Wimmer.

MakePersistentLength(p0, p1, p2, bladeHeight);      //Function body in the appendix

A width $w$ for each control point defines the width of the grass blade. To apply the width, we translate each control point outwards by length $w$ using the perpendicular vector of our bladeDirection. The new projected control points are called $P_0^-$ , $P_0^+$ , $P_1^-$ , $P_1^+$ , $P_2^-$ and $P_2^+$ . All positive $P^+$ form a blade edge, and all negative $P^-$ form the other one. Thus, we now have two Bézier curves representing the edges of the grass blade as can be seen in the following figure

Bezier Blade

贝塞尔曲线到三角形

To create geometry, we evaluate each of our two edge curves $n=4$ times. Thus we get $4$ vertices per blade edge, or $8$ vertices in total. A Bézier curve can be evaluated as follows

float3 bezier(float3 p0, float3 p1, float3 p2, float t)
{
    float3 a = lerp(p0, p1, t);
    float3 b = lerp(p1, p2, t);
    return lerp(a, b, t);
}

Connecting these $|V|=8$ vertices results in $|T|=6$ triangles.

Assuming a counter-clockwise winding order, this results in the following primitives

图元	0	1	2	3	4	5
i0	0	3	2	5	4	7
i1	1	2	3	4	5	6
i2	2	1	4	3	6	5

To perform shading, we calculate the normal vectors, depending on the derivative of the Bézier curve

float3 bezierDerivative(float3 p0, float3 p1, float3 p2, float t)
{
    return 2. * (1. - t) * (p1 - p0) + 2. * t * (p2 - p1);
}

To get the normal vector, we first need to calculate a normalized vector perpendicular to the bladeDirection. We then calculate the cross product between this sideVec and the derivative at the current interpolation parameter t.

float3 sideVec = normalize(float3(bladeDirection.y, -bladeDirection.x, 0));
float3 normal  = cross(sideVec, normalize(bezierDerivative(p0, p1, p2, t)));

将草叶组合成草丛

One mesh shader work group generates the geometry for one patch of grass. A patch of grass has the following arguments

struct GrassPatchArguments {
    float3 patchPosition;
    float3 groundNormal;
    float  height;
};

We assume the buffer of GrassPatchArguments as given. We access the buffer at the index of gid, with gid being the SV_GroupID of our thread group. We randomly scatter the blades of grass in a circle around patchPosition. Since the ground we place the grass on typically is not flat, blades further away from the patchPosition would start floating mid air. To fix this, we require the groundNormal to project the blade scattering circle onto the terrain surface. The variable patchRadius is a global parameter and describes the radius of the scattering circle, thus the maximum distance to the center of the grass patch. To calculate the patchPosition of a blade of grass in a patch, we obtain a random radius $r_\{\mathrm{blade}}$ (bladeRadius) and a random angle $\alpha$ (alpha). With these, we can calculate the bladeOffset from the center of the patch patchPosition. Each blade is then rotated with a random angle $\beta$ (beta).

In the following code example, we compute bladeDirection and bladePosition. Note that the function rand(...) provides a seeded and uniformly distributed pseudo-random value between $0$ and $1$ .

    ...
    uint seed = combineSeed(globalSeed, bladeId);

    float beta = 2. * PI * rand(seed);
    float2 bladeDirection = float2(cos(beta), sin(beta));

    float3 tangent = normalize(cross(float3(0,1,0),groundNormal));
    float3 bitangent = normalize(cross(groundNormal, tangent));

    float alpha = 2. * PI * rand(seed);
    float bladeRadius = patchRadius * sqrt(rand(seed));
    float3 bladeOffset = bladeRadius * (cos(alpha) * tangent + sin(alpha) * bitangent);

    float3 bladePosition = patchPosition + bladeOffset;
    ...

We also get a height for the whole patch, which is the mean height of all grass blades of the patch. For a more diverse appearance, we slightly vary the height of each grass blade in a patch

const float bladeHeight = height + float(rand(seed)) * RAND_HEIGHT_SCALE;

线程分配

由于 DirectX-Specs 中规定网格着色器（mesh shader）最多只能输出 $256$ 个顶点，因此我们的草地块包含最多 $\frac{256}{8}=32$ 根草叶。我们有 $6$ 个图元和每根草叶 $8$ 个顶点。这导致每块草地有 $192$ 个图元和 $256$ 个顶点。我们的顶点具有以下属性

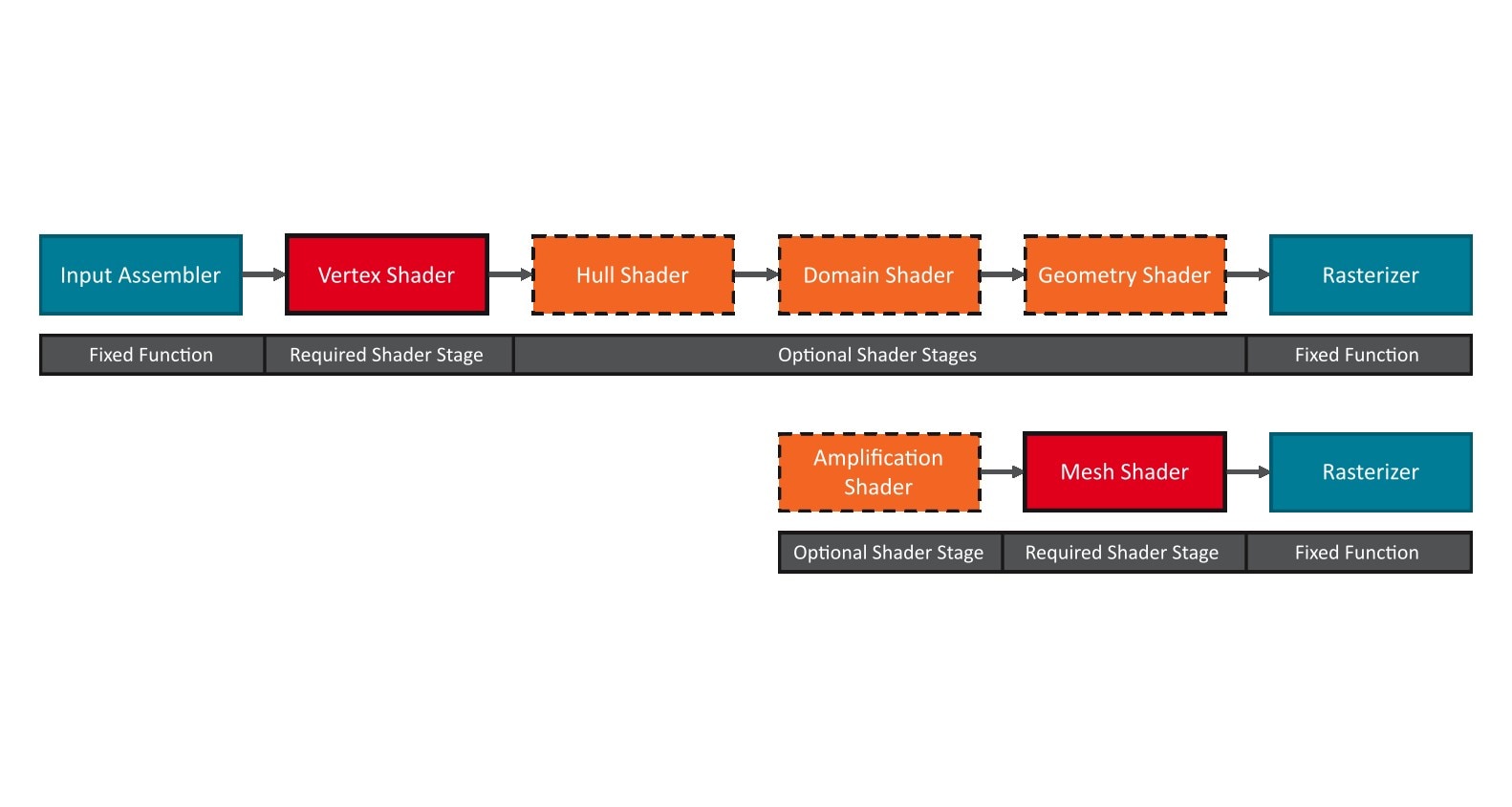
struct Vertex
{
    float4 clipSpacePosition   : SV_POSITION;
    float3 worldSpacePosition  : POSITION0;
    float3 worldSpaceNormal    : NORMAL0;
    float  rootHeight          : BLENDWEIGHT0; //Used for fake self shadow
    float  height              : BLENDWEIGHT1; //Used for fake self shadow
};

要编写索引和顶点缓冲区，我们使用了本系列早期博文 Mesh Shader Opimizations and Best Practices 中描述的最佳实践。简而言之，我们将线程组大小设置为其限制值 GROUP_SIZE = $128$ 。我们必须确保 $i$ -th 图元和 $i$ -th 顶点由线程组中的 $i$ -th 线程写入。由于我们的图元数量大于 $128$ 的线程组大小，我们使用 $128$ 的线程组侧步长。每个线程最多计算两个顶点和两个图元。

写入顶点缓冲区

首先，我们根据组线程 ID gtid 来看顶点是如何生成和写入的。

...
for (uint i = 0; i < 2; ++i) {
    int vertId = gtid + GROUP_SIZE * i;

    if(vertId >= vertexCount) break;            //Depends on the number of blades generated

    int bladeId     = vertId / verticesPerBlade;
    int vertIdLocal = vertId % verticesPerBlade;
    ...

通过这个 for 循环，我们每个线程最多运行两次。当 vertId 大于我们要生成的顶点数 $|V|=256$ 时，我们退出循环。通过这种算术，组中的每个线程在第一次循环迭代中计算以下值：

GTID	0	1	2	3	4	5	6	7	8	9	10	11	12
vertId	0	1	2	3	4	5	6	7	8	9	10	11	12
bladeId	0	0	0	0	0	0	0	0	1	1	1	1	1
vertIdLocal	0	1	2	3	4	5	6	7	0	1	2	3	4
offsetSign	-	+	-	+	-	+	-	+	-	+	-	+	-
t	$0$	$0$	$\frac{1}{3}$	$\frac{1}{3}$	$\frac{2}{3}$	$\frac{2}{3}$	$1$	$1$	$0$	$0$	$\frac{1}{3}$	$\frac{1}{3}$	$\frac{2}{3}$

在第二次迭代中，vertId 偏移了 GROUP_SIZE = $128$

GTID	0	1	2	3	4	5	6	7	8	9	10	11	12
vertId	128	129	130	131	132	133	134	135	136	137	138	139	140
bladeId	16	16	16	16	16	16	16	16	17	17	17	17	17
vertIdLocal	0	1	2	3	4	5	6	7	0	1	2	3	4
offsetSign	-	+	-	+	-	+	-	+	-	+	-	+	-
t	$0$	$0$	$\frac{1}{3}$	$\frac{1}{3}$	$\frac{2}{3}$	$\frac{2}{3}$	$1$	$1$	$0$	$0$	$\frac{1}{3}$	$\frac{1}{3}$	$\frac{2}{3}$

使用 gtid 的最大值 $127$ ，我们得到变量的以下范围：

值	Range
`vertID`	$0..255$
`bladeId`	$0..31$
`vertIdLocal`	$0..7$

有了这些值，我们就可以确定需要生成哪个顶点。但首先，我们从 GrassPatchArguments 生成控制点。根据我们的 vertIdLocal，我们会将控制点 $P$ 修改为 $P^-$ 或 $P^+$

    //vector perpendicular to the blade direction
    float3 sideVec = normalize(float3(bladeDirection.y, -bladeDirection.x, 0));
    float3 offset  = tsign(vertIdLocal, 0) * WIDTH_SCALE * sideVec;

    const static float w0 = 1.f;
    const static float w1 = .7f;
    const static float w2 = .3f;

    p0 += offset * w0;
    p1 += offset * w1;
    p2 += offset * w2;

实用函数 tsign(uint value, int bitPos) 返回 $-1$ 或 $+1$ ，具体取决于 value 中 bitPos 位是否设置。因此，当 vertIdLocal 为偶数时，我们将 $P$ 向负方向移动，当 vertIdLocal 为奇数时，向正方向移动。我们分别用 $w_0$ , $w_1$ 和 $w_2$ 进行缩放。

由于我们在 $4$ 个位置评估贝塞尔曲线，因此我们需要 $4$ 个不同的插值参数 t 值。

    float t = (vertIdLocal/2) / float(verticesPerBladeEdge - 1);

    Vertex vertex;
    vertex.height             = height;
    vertex.rootHeight         = p0.z;
    vertex.worldSpacePosition = bezier(p0, p1, p2, t);
    vertex.worldSpaceNormal   = cross(sideVec, normalize(bezierDerivative(p0, p1, p2, t)));
    vertex.clipSpacePosition  = mul(DynamicConst.viewProjectionMatrix, float4(vertex.worldSpacePosition, 1));

    verts[vertId] = vertex;
}   //end for-loop
...

前面的表格显示了这些 t 的不同值，具体取决于 gtid 和 i。在计算出每个所需的值之后，我们将顶点写入输出缓冲区中的索引 vertId。

我们可以看到，第一个 gtid = $0$ 的线程写入顶点 vertId = $0$ 和顶点 vertId = $128$ 。

写入索引缓冲区

写入索引缓冲区与写入顶点缓冲区的工作方式类似。图元的拓扑结构在 Bézier to triangles 中进行了描述。

for (uint i = 0; i < 2; ++i) {
    int triId = gtid + GROUP_SIZE * i;

    if (triId >= triangleCount) break;

    int bladeId    = triId / trianglesPerBlade;
    int triIdLocal = triId % trianglesPerBlade;

与我们创建顶点 ID 的方式类似，我们生成三角形 ID：我们不除以 verticesPerBlade，而是除以 trianglesPerBlade。

    int offset = bladeId * verticesPerBlade + 2 * (triIdLocal / 2);

    uint3 triangleIndices = (triLocal & 1) == 0? uint3(0, 1, 2) :
                                                 uint3(3, 2, 1);

    tris[triId] = offset + triangleIndices;
}   //end for-loop

offset 取决于顶点，因此我们乘以 verticesPerBlade。根据 triIdLocal 是偶数还是奇数，我们写入四边形的右侧或左侧三角形。

下表显示了 gtid 如何映射到写入的图元。

GTID	0	1	2	3	4	5	6	7	8	9	10	11
triId	0	1	2	3	4	5	6	7	8	9	10	11
bladeId	0	0	0	0	0	0	1	1	1	1	1	1
triIdLocal	0	1	2	3	4	5	0	1	2	3	4	5
offset	0	0	2	2	4	4	8	8	10	10	12	12
图元	`(0,1,2)`	`(3,2,1)`	`(2,3,4)`	`(5,4,3)`	`(4,5,6)`	`(7,6,5)`	`(8,9,10)`	`(11,10,9)`	`(10,11,12)`	`(13,12,11)`	`(12,13,14)`	`(15,14,13)`

我们可以看到，第一个 gtid = $0$ 的线程在索引缓冲区的第一个图元处写入 triId = $0$ 。而在第二次迭代中，它在 triId = $128$ 处写入。

细节级别

为了提高我们的草地网格着色器的性能，我们减少了当草地块离相机越远时渲染的几何图形量。为此，我们在远处减少草叶的数量。为了弥补这一点，我们增加了整个草地块的剩余草叶的宽度。

分数缩放

为了隐藏过渡，我们实现了草叶数量的分数缩放。为此，我们引入了两个变量 bladeCount 和其真实值版本 bladeCountF。

...
float bladeCountF = lerp(float(MAX_BLADE_COUNT), 2., saturate(distanceToCamera / GRASS_END_DISTANCE));
int   bladeCount  = ceil(bladeCountF);

if (bladeId == (bladeCount - 1)) {
    width *= frac(bladeCountF);
}
...

所有 bladeId 小于 bladeCount-1 的草叶都将被 unmodified 地绘制。最后一根草叶 bladeId = bladeCount-1 的宽度将根据 bladeCountF 的小数部分进行缩放。

无分数缩放	有分数缩放

几何体补偿

为了保持草地在与相机距离不同的情况下视觉外观的一致性，我们修改了草地块中每根草叶的宽度。

width *= maxBladeCount / bladeCountF;

动画极大地夸张地展示了这种效果，但在茂密的草地上，这种效果几乎不引人注意。

夸张的加宽效果

风力动画

为了模拟风的效果，我们采用了一种简单的方法，该方法受到了 Guerrilla Games 的 Gilbert Sanders 在 GDC 演讲 Between Tech and Art: The Vegetation of Horizon Zero Dawn 的启发，该方法在 $x$ 和 $y$ 方向上使用了正弦波。为了增强效果，我们在时间上添加了一些 Perlin 噪声。

float3 GetWindOffset(float2 pos, float time){
    float posOnSineWave = cos(WindDirection) * pos.x - sin(WindDirection) * pos.y;

    float t     = time + posOnSineWave + 4 * PerlinNoise2D(0.1 * pos);
    float windx = 2 * sin(.5 * t);
    float windy = 1 * sin(1. * t);

    return ANIMATION_SCALE * float3(windx, windy, 0);
}

单块草地的风力效果	草地的风力效果

像素着色器

为了改善草地的着色外观，我们利用了两个简单技巧：首先，我们通过使草根附近的草变暗来模拟自阴影效果。其次，我们应用 Perlin 噪声在草地上创建深色斑块。

自阴影	Perlin 噪声草地颜色

...
static const float3 grassGreen = float3(0.41, 0.44, 0.29);

float selfshadow     = clamp(pow((input.worldSpacePosition.y - input.rootHeight) / input.height, 1.5), 0, 1);
output.baseColor.rgb = pow(grassGreen, 2.2) * selfshadow;
output.baseColor.rgb *= 0.75 + 0.25 * PerlinNoise2D(0.25 * input.worldSpacePosition.xz);
...

请注意，由于我们使用延迟渲染器进行开发，因此实际着色的实现留给读者。我们根据像素距离草叶根部的高度来使像素变暗，并根据其世界空间位置应用 Perlin 噪声。

此外，通过实验，我们发现将草的法线与向上向量进行插值可以使草叶看起来更柔和。

output.normal.xyz = normalize(lerp(float3(0, 0, 1), normal, 0.25));

未来工作

我们的草地系统可以在许多不同领域进行扩展和改进。

季节性效果
通过对 $P_2$ 应用向下的力，我们可以模拟季节的影响。在较暖和的季节，草具有更强的弹力。在较冷的季节，草的硬度较低，更贴近地面。

进一步的几何体减少
为了进一步减少远处的几何体，我们可以实现一个稀疏草着色器。该着色器将使用公告牌（billboarding）技术，以更少的几何体模拟草的外观。

其他类型的植被
可以修改网格着色器以生成不同类型的植被。这可以包括不同种类的草、花、灌木和其他杂物。

结论

在这篇博文中，我们描述了如何使用网格着色器生成草地。我们解释了如何用贝塞尔曲线表示草，以及如何有效地将生成的几何体写入索引和顶点缓冲区。我们提供了根据相机距离减少几何体数量的方法，并说明了如何动画化草在风中的移动。我们描述了一个简单的像素着色器实现来改善草地的视觉效果。最后，我们提供了一些关于如何改进我们实现的想法。

附录

完整草网格着色器

int tsign(in uint gtid, in int id) {
    return (gtid & (1u << id)) ? 1 : -1;
}

struct Vertex
{
    float4 clipSpacePosition   : SV_POSITION;
    float3 worldSpacePosition  : POSITION0;
    float3 worldSpaceNormal    : NORMAL0;
    float  rootHeight          : BLENDWEIGHT0;
    float  height              : BLENDWEIGHT1;
};

static const int GROUP_SIZE       = 128;
static const int GRASS_VERT_COUNT = 256;
static const int GRASS_PRIM_COUNT = 192;

[NumThreads(GROUP_SIZE, 1, 1)]
[OutputTopology("triangle")]
void MeshShader(
    uint gtid : SV_GroupThreadID,
    uint gid : SV_GroupID,
    out indices uint3 tris[GRASS_PRIM_COUNT],
    out vertices Vertex verts[GRASS_VERT_COUNT]
)
{
    const GrassPatchArguments arguments = //Load arguments

    SetMeshOutputCounts(GRASS_VERT_COUNT, GRASS_PRIM_COUNT);

  static const int verticesPerBladeEdge = 4;
    static const int verticesPerBlade =  2 * verticesPerBladeEdge;
    static const int trianglesPerBlade = 6;
    static const int maxBladeCount = 32;

    const float3 patchCenter = arguments.position;
    const float3 patchNormal = arguments.normal;
    const float  spacing     = DynamicConst.grassSpacing;
    const int seed           = combineSeed(asuint(int(patchCenter.x / spacing)), asuint(int(patchCenter.y / spacing)));

    float distanceToCamera = distance(arguments.position, DynamicConst.cullingCameraPosition.xyz);
    float bladeCountF      = lerp(float(maxBladeCount), 2., pow(saturate(distanceToCamera / (GRASS_END_DISTANCE * 1.05)), 0.75));

    int bladeCount = ceil(bladeCountF);

    const int vertexCount   = bladeCount * verticesPerBlade;
    const int triangleCount = bladeCount * trianglesPerBlade;

    for (uint i = 0; i < 2; ++i){
        int vertId = gtid + GROUP_SIZE * i;

        if (vertId >= vertexCount) break;

        int bladeId     = vertId / verticesPerBlade;
        int vertIdLocal = vertId % verticesPerBlade;

        const float height = arguments.height + float(rand(seed, bladeId, 20)) / 40.;

        //position the grass in a circle around the patchPosition and angled using the patchNormal
        float3 tangent   = normalize(cross(float3(0, 1, 0), patchNormal));
        float3 bitangent = normalize(cross(patchNormal, tangent));

        float  bladeDirectionAngle = 2. * PI * rand(seed, 4, bladeId);
        float2 bladeDirection      = float2(cos(bladeDirectionAngle), sin(bladeDirectionAngle));

        float  offsetAngle  = 2. * PI * rand(seed, bladeId);
        float  offsetRadius = spacing * sqrt(rand(seed, 19, bladeId));
        float3 bladeOffset  = offsetRadius * (cos(offsetAngle) * tangent + sin(offsetAngle) * bitangent);

        float3 p0 = patchCenter + bladeOffset;
        float3 p1 = p0 + float3(0, 0, height);
        float3 p2 = p1 + bladeDirection  * height * 0.3;

        p2 += GetWindOffset(p0.xy, DynamicConst.shaderTime);

        MakePersistentLength(p0, p1, p2, height);

        float width = 0.03;

        width *= maxBladeCount / bladeCountF;

        if (bladeId == (bladeCount-1)){
            width *= frac(bladeCountF);
        }

        Vertex vertex;
        vertex.height                 = arguments.height;
        vertex.worldSpaceGroundNormal = arguments.normal;
        vertex.rootHeight             = p0.z;

        float3 sideVec = normalize(float3(bladeDirection.y, -bladeDirection.x, 0));
        float3 offset  = tsign(vertIdLocal, 0) * width * sideVec;

        p0 += offset * 1.0;
        p1 += offset * 0.7;
        p2 += offset * 0.3;

        float t = (vertIdLocal/2) / float(verticesPerBladeEdge - 1);
        vertex.worldSpacePosition = bezier(p0, p1, p2, t);
        vertex.worldSpaceNormal   = cross(sideVec, normalize(bezierDerivative(p0, p1, p2, t)));
        vertex.clipSpacePosition  = mul(DynamicConst.viewProjectionMatrix, float4(vertex.worldSpacePosition, 1));

        verts[vertId] = vertex;
    }

    for (uint i = 0; i < 2; ++i){
        int triId = gtid + GROUP_SIZE * i;

        if (triId >= triangleCount) break;

        int bladeId    = triId / trianglesPerBlade;
        int triIdLocal = triId % trianglesPerBlade;

        int offset = bladeId * verticesPerBlade + 2 * (triIdLocal / 2);

        uint3 triangleIndices = (triLocal & 1) == 0? uint3(0, 1, 2) :
                                                     uint3(3, 2, 1);

        tris[triId] = offset + triangleIndices;
    }
}

完整像素着色器

struct PixelShaderOutput {
    float3 patchPosition : SV_Target0;
    float4 baseColor : SV_Target1;
    float3 normal : SV_Target2;
};


PixelShaderOutput GrassPatchPixelShader(const Vertex input, bool isFrontFace : SV_IsFrontFace)
{
    PixelShaderOutput output;
    output.position = input.worldSpacePosition;

    float selfshadow = clamp(pow((input.worldSpacePosition.y - input.rootHeight)/input.height, 1.5), 0, 1);
    output.baseColor.rgb = pow(float3(0.41, 0.44, 0.29), 2.2) * selfshadow;
    output.baseColor.rgb *= 0.75 + 0.25 * PerlinNoise2D(0.25 * input.worldSpacePosition.xy);
    output.baseColor.a = 1;

    float3 normal = normalize(input.worldSpaceNormal);

    if (!isFrontFace) {
        normal = -normal;
    }

    output.normal.xyz = normalize(lerp(float3(0, 0, 1), normal, 0.25));

    return output;
}

保持恒定长度

MakePersistentLength Source

void MakePersistentLength(in float3 v0, inout float3 v1, inout float3 v2, in float height)
{
    //Persistent length
    float3 v01 = v1 - v0;
    float3 v12 = v2 - v1;
    float lv01 = length(v01);
    float lv12 = length(v12);

    float L1 = lv01 + lv12;
    float L0 = length(v2-v0);
    float L = (2.0f * L0 + L1) / 3.0f; //http://steve.hollasch.net/cgindex/curves/cbezarclen.html

    float ldiff = height / L;
    v01 = v01 * ldiff;
    v12 = v12 * ldiff;
    v1 = v0 + v01;
    v2 = v1 + v12;
}