在上一篇关于拉普拉斯算子的帖子中,我们开发了一个基于拉普拉斯算子的有限差分模板代码的 HIP 实现。最初的实现发现是受内存带宽限制的,这意味着其运行时间受限于数据与全局内存之间传输的速率。此外,当前的内存访问模式需要多次访问全局内存才能加载所有数据,因此如果我们可以缓存更多数据,执行时间就可以缩短。我们将图(FOM)定义为*有效内存带宽*,即将理论内存移动量除以实际执行时间。我们 HIP 实现的 FOM 目前达到了单块 MI250X GCD 峰值的 50%[1],但我们的分析表明,将实际内存移动量减少到理论值,可能会使我们的 FOM 达到峰值的至少 71%[1]。在本帖中,我们将介绍两种可应用于内核以帮助实现此目标的常见优化。
-
循环分块以显式减少内存加载
-
重新排序内存访问模式以提高缓存效率
回顾
在上一篇帖子中,我们考虑了拉普拉斯算子的中心有限差分模板的 HIP 实现。回想一下,拉普拉斯算子的形式是一个标量场 u(x,y,z) 的散度梯度:
∇⋅∇u=∇2u=∂x2∂2u+∂y2∂2u+∂z2∂2u最初的 HIP 实现如下所示
template <typename T>__global__ void laplacian_kernel(T * f, const T * u, int nx, int ny, int nz, T invhx2, T invhy2, T invhz2, T invhxyz2) {
int i = threadIdx.x + blockIdx.x * blockDim.x; int j = threadIdx.y + blockIdx.y * blockDim.y; int k = threadIdx.z + blockIdx.z * blockDim.z;
// Exit if this thread is on the boundary if (i == 0 || i >= nx - 1 || j == 0 || j >= ny - 1 || k == 0 || k >= nz - 1) return;
const int slice = nx * ny; size_t pos = i + nx * j + slice * k;
// Compute the result of the stencil operation f[pos] = u[pos] * invhxyz2 + (u[pos - 1] + u[pos + 1]) * invhx2 + (u[pos - nx] + u[pos + nx]) * invhy2 + (u[pos - slice] + u[pos + slice]) * invhz2;}
template <typename T>void laplacian(T *d_f, T *d_u, int nx, int ny, int nz, int BLK_X, int BLK_Y, int BLK_Z, T hx, T hy, T hz) {
dim3 block(BLK_X, BLK_Y, BLK_Z); dim3 grid((nx - 1) / block.x + 1, (ny - 1) / block.y + 1, (nz - 1) / block.z + 1); T invhx2 = (T)1./hx/hx; T invhy2 = (T)1./hy/hy; T invhz2 = (T)1./hz/hz; T invhxyz2 = -2. * (invhx2 + invhy2 + invhz2);
laplacian_kernel<<<grid, block>>>(d_f, d_u, nx, ny, nz, invhx2, invhy2, invhz2, invhxyz2);}以及在单块 MI250X GCD 上的相应性能
$ ./laplacian_dp_kernel1Kernel: 1Precision: doublenx,ny,nz = 512, 512, 512block sizes = 256, 1, 1Laplacian kernel took: 2.64172 ms, effective memory bandwidth: 808.148 GB/s报告的 `808.148 GB/s` 达到了我们上一篇帖子中设定的目标值的 69.4%。我们将继续使用 `rocprof` 来帮助我们评估以下各项优化的有效性。
在上一篇帖子中,我们可以推断出设备数组 `f` 的存储是高效的,因为 `WRITE_SIZE` 指标与理论值匹配。然而,报告的 `FETCH_SIZE` 几乎是理论值的两倍,因此如果能减小这个数据量,就有可能提高性能。回想一下,更新 `f` 数组中的每个条目都需要加载 `u` 数组中的七个元素,但每个 `u` 元素最多可以被相邻的网格点重用六次。需要注意的是,从波前(wavefront)的角度来看,每个 `u` 条目的加载是一个连续的 64 个条目块。我们当前的线程块配置(256 × 1 × 1)沿 `x` 方向加载四个波前的元素,这为单个波前的线程提供了缓存和重用 `x - 1` 和 `x + 1` 模板计算的 `x` 元素的机会。然而,沿 `y` 和 `z` 方向加载波前必须小心实现,以最大化空间局部性和重用来自相邻波前和线程块的值。因此,我们将注意力集中在其中一个方向的优化加载,即通过循环分块。
循环分块
目前,每个线程计算围绕单个网格点的模板。如果我们让每个线程计算多个网格点的模板会怎样?这将需要每个线程执行更多的加载指令,但由于线程的连续性,这些加载更有可能重用寄存器中已缓存的 `u` 值。这种优化称为循环分块,它将减少启动的线程块数量,并增加每个线程计算的模板数量。
在我们深入研究优化的拉普拉斯内核之前,让我们先看一个简单的例子来进一步解释循环分块的概念和好处:假设我们要执行步长计算 `f[pos] = u[pos - 1] + u[pos] + u[pos + 1]`。如果不进行分块,每个线程将需要执行三个加载和一个存储指令。如果每个线程只加载一个 `u` 元素,并重用已加载和存储在寄存器中的另外两个 `u` 元素,那将是理想的。换句话说,我们应该尽量减少每个线程每存储指令的加载次数。如果我们按某个因子分块,假设选择 2,那么每个线程将执行两次存储,但考虑加载次数:
f[pos] = u[pos - 1] + u[pos] + u[pos + 1]f[pos + 1] = u[pos] + u[pos + 1] + u[pos + 2]注意 `u[pos]` 和 `u[pos + 1]` 出现了两次,这意味着我们只需要加载它们一次。这个观察使我们能够重用先前加载的值。为了清楚地说明这一点,我们可以引入两个变量:
double u0 = u[pos];double u1 = u[pos + 1]f[pos] = u[pos - 1] + u0 + u1f[pos + 1] = u0 + u1 + u[pos + 2]结果,我们将加载指令的数量从 6 减少到 4(即减少 33%)。我们现在大约有 2 次加载/存储。请参阅下表,了解循环分块因子与加载/存储比率的关系。
块因子 | 加载 | 存储 | 比率 |
|---|---|---|---|
1 | 3 | 1 | 3.00 |
2 | 4 | 2 | 2.00 |
4 | 6 | 4 | 1.50 |
8 | 10 | 8 | 1.25 |
16 | 18 | 16 | 1.13 |
请注意,增加块因子会增加内核中的寄存器使用量,从而降低其占用率。如果编译器耗尽寄存器,就会发生寄存器溢出到全局内存的情况,这可能会对性能产生负面影响。
回到 3D 拉普拉斯算子内核,有三个潜在的循环分块方向。我们以 `y` 方向为例进行演示。考虑下图,说明每个线程在 `xy` 平面上的重用模式:
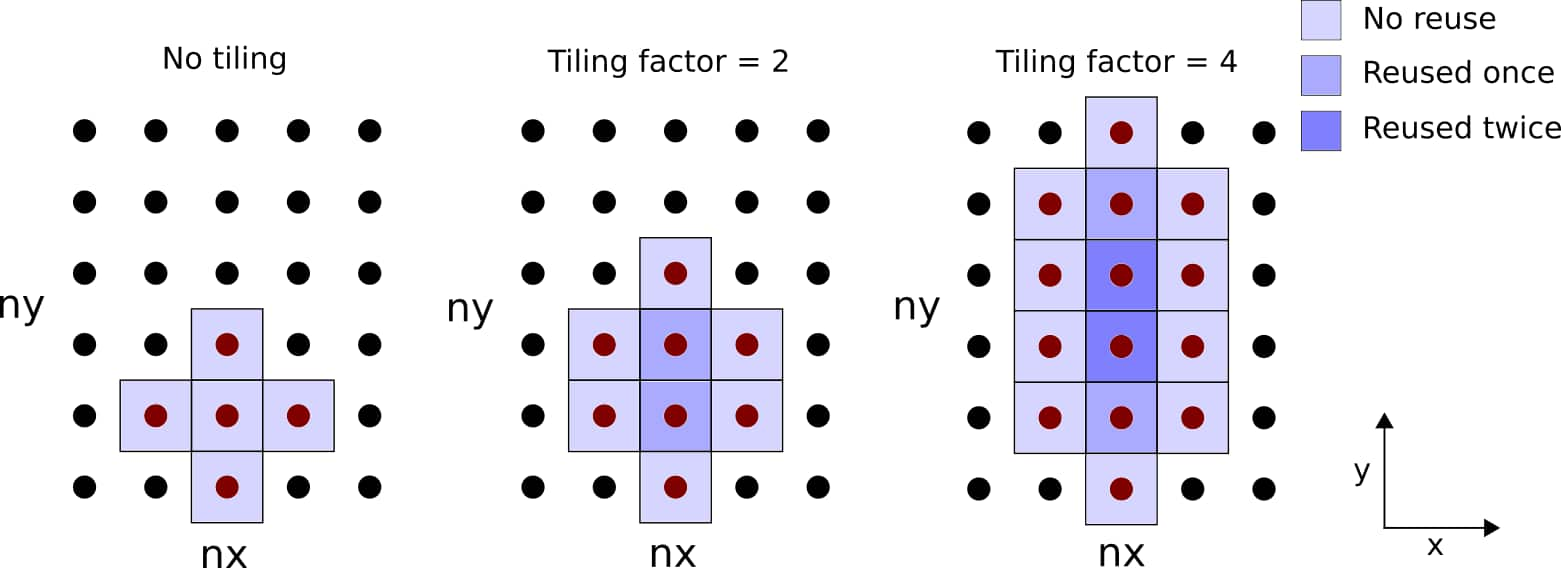
图 1:图示了每个线程在 `xy` 平面上的循环分块。加载和重用的网格点数量取决于块宽度。
我们用 `m` 表示块因子,它是一个在编译时确定的用户定义宏变量。对该内核的代码修改可能相当复杂,因此我们将分两个阶段介绍更改:设置和计算。首先,我们应用以下更改:
| 内核 1 设置(之前) | 内核 2 设置(之后) |
|---|---|
| |
内核 2 引入了宏变量 `m`,用于划分 `y` 方向的网格维度。将 `m=1` 设置为当前没有分块效果 – 尝试其他值需要重新编译代码。对于模板与边界重叠的情况,我们消除了线程在 `y` 边界退出的要求。
在下一组代码修改中,我们将重点重写 `m` 块因子的 `f[pos] = …` 计算。由于我们在 `y` 方向进行分块,每个线程将 `pos` 步长设置为 `nx`。这些修改很棘手,所以我们将它们分解为四个步骤:
-
在主计算内核中添加一个 for 循环
-
引入一个大小为 `m` 的数组来累积模板点的运行总和
-
将 `u` 元素加载和 `f` 元素存储拆分为单独的循环
-
引入一个变量来保存一个 `u` 元素以供重用
下面是应用这四个步骤之前和之后的代码片段。我们首先将模板评估包装在一个 for 循环中:
| 内核 1 计算 – 步骤 0(之前) | 步骤 1(之后) |
|---|---|
| |
引入一个编译时已知的值为 `m` 的 for 循环,其效果类似于循环展开,编译器将最小化循环开销。请记住,`m` 不能太大,否则编译器会将寄存器溢出到全局内存。
此时,内核在技术上是分块的,但是,还需要一些代码修改来最小化加载到存储的比率。接下来,我们创建一个累积数组:
| 步骤 1(之前) | 步骤 2(之后) |
|---|---|
| |
累积数组 `Lu` 临时保存计算的总和。请注意,我们保留了模板计算的原始顺序 – 先加载 `x` 方向的模板,然后是 `y` 方向的模板,最后是 `z` 方向的模板。我们最终会重新审视这个顺序,但下一步是将加载和存储步骤分开:
| 步骤 2(之前) | 步骤 3(之后) |
|---|---|
| |
将加载和存储分成单独的 for 循环,可以使所有 `Lu` 元素同时累积模板计算,然后再写入 `f`。第四个也是最后一个更改是通过重用不同模板之间的已加载 `u` 元素来显式删除加载指令。`n` 的每次迭代仍然加载 `Lu[n]` 的 `x` 方向和 `z` 方向模板,但现在可能重用 `u` 元素来计算属于 `Lu[n-1]` 和/或 `Lu[n+1]` 的 `y` 方向模板:
| 步骤 3(之前) | 内核 2 计算 – 步骤 4(之后) |
|---|---|
| |
以下是捕获上述所有代码修改的完整内核 2 实现:
// Tiling factor#define m 1template <typename T>__global__ void laplacian_kernel(T * f, const T * u, int nx, int ny, int nz, T invhx2, T invhy2, T invhz2, T invhxyz2) {
int i = threadIdx.x + blockIdx.x * blockDim.x; int j = m*(threadIdx.y + blockIdx.y * blockDim.y); int k = threadIdx.z + blockIdx.z * blockDim.z;
// Exit if this thread is on the xz boundary if (i == 0 || i >= nx - 1 || k == 0 || k >= nz - 1) return;
const int slice = nx * ny; size_t pos = i + nx * j + slice * k;
// Each thread accumulates m stencils in the y direction T Lu[m] = {0};
// Scalar for reusable data T center;
// Loop tiling for (int n = 0; n < m; n++) { center = u[pos + n*nx]; // store for reuse
// x direction Lu[n] += center *invhxyz2 + (u[pos - 1 + n*nx] + u[pos + 1 + n*nx]) * invhx2;
// y - 1, first n if (n == 0) Lu[n] += u[pos - nx + n*nx] * invhy2;
// reuse: y + 1 for prev n if (n > 0) Lu[n-1] += center * invhy2;
// reuse: y - 1 for next n if (n < m - 1) Lu[n+1] += center * invhy2;
// y + 1, last n if (n == m - 1) Lu[n] += u[pos + nx + n*nx] * invhy2;
// z - 1 and z + 1 Lu[n] += (u[pos - slice + n*nx] + u[pos + slice + n*nx]) * invhz2; }
// Store only if thread is inside y boundary for (int n = 0; n < m; n++) if (j + n > 0 && j + n < ny - 1) f[pos + n*nx] = Lu[n]; }
template <typename T>void laplacian(T *d_f, T *d_u, int nx, int ny, int nz, int BLK_X, int BLK_Y, int BLK_Z, T hx, T hy, T hz) {
dim3 block(BLK_X, BLK_Y, BLK_Z); dim3 grid((nx - 1) / block.x + 1, (ny - 1) / (block.y * m) + 1, (nz - 1) / block.z + 1); T invhx2 = (T)1./hx/hx; T invhy2 = (T)1./hy/hy; T invhz2 = (T)1./hz/hz; T invhxyz2 = -2. * (invhx2 + invhy2 + invhz2);
laplacian_kernel<<<grid, block>>>(d_f, d_u, nx, ny, nz, invhx2, invhy2, invhz2, invhxyz2);}请注意,此内核当前编写为 `ny` 必须能被 `block.y * m` 整除。让我们尝试使用与我们选择的问题大小兼容的各种 `m` 值,看看循环分块是否能带来任何好处。
加速 | 目标值百分比 | |
|---|---|---|
内核 1 – 基线 | 1.00 | 69.4% |
内核 2 – 循环分块 m=1 | 1.00 | 69.4% |
内核 2 – 循环分块 m=2 | 0.98 | 68.3% |
内核 2 – 循环分块 m=4 | 0.94 | 65.5% |
内核 2 – 循环分块 m=8 | 0.92 | 64.0% |
内核 2 – 循环分块 m=16 | 0.29 | 20.1% |
令人奇怪的是,检查过的所有 `m` 值都没有带来任何显著的加速。事实上,增加块因子似乎会加剧性能问题。让我们检查 `FETCH_SIZE` 和 `L2CacheHit` 指标以获得更多见解:
FETCH_SIZE (GB) | 获取效率 (%) | L2CacheHit (%) | |
|---|---|---|---|
理论值 | 1.074 | – | – |
内核 1 – 基线 | 2.014 | 53.3 | 65.0 |
内核 2 – 循环分块 m=1 | 2.014 | 53.3 | 65.0 |
内核 2 – 循环分块 m=2 | 1.848 | 58.1 | 60.5 |
内核 2 – 循环分块 m=4 | 1.880 | 57.1 | 57.0 |
内核 2 – 循环分块 m=8 | 1.820 | 59.0 | 56.0 |
内核 2 – 循环分块 m=16 | 5.637 | 19.1 | 40.9 |
获取效率仅略有提高,而 L2 缓存命中率显着下降。我们怀疑原因是累积步骤遵循了与初始内核相同的访问模式。也就是说,我们首先计算 `x` 方向的模板,然后是可能可重用的 `y - 1` 和 `y + 1` 模板,最后是 `z - 1` 和 `z + 1` 模板。从内存地址的角度来看,读取访问模式向前和向后跳转,这可能会产生影响,如下一节所述。
重新排序读取访问模式
优化后,加速几乎没有或没有。虽然增加块因子减小了加载/存储比率,但并不一定能转化为全局数据移动的减少。为了使 `FETCH_SIZE` 减小,L2 与全局内存之间的数据移动必须减小。随着加载/存储比率的增加,发送到 L1 的读取请求数量必须减少,L2 的请求数量也必须减少(假设 L1 缓存命中率保持不变)。由于我们观察到 `FETCH_SIZE` 保持不变且 `L2CacheHit` 下降,因此该优化减少了 L2 缓存的压力(发送到它的请求更少),但未能提高从全局内存加载到 L2 缓存的数据的重用性。为了理解为什么之前的内核不能最佳地重用 L2 数据,让我们可视化 3D 模板及其读取访问模式(如果 `m = 2`):
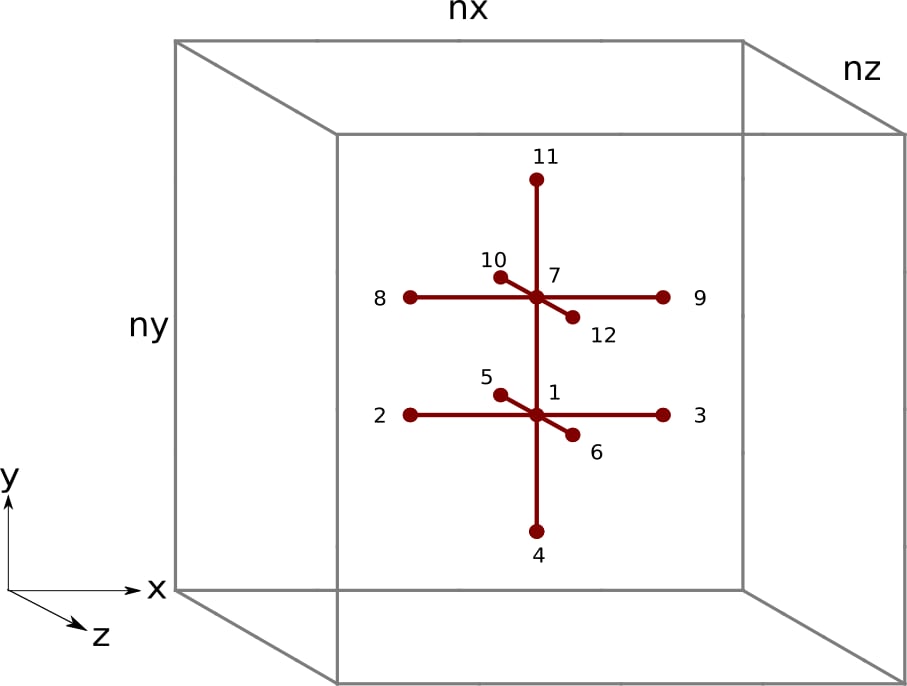
图 2:3D 空间中的有限差分模板,块因子为 `m = 2`。黑色的数字表示内核 2 中的每个线程访问 `u` 元素 的顺序。
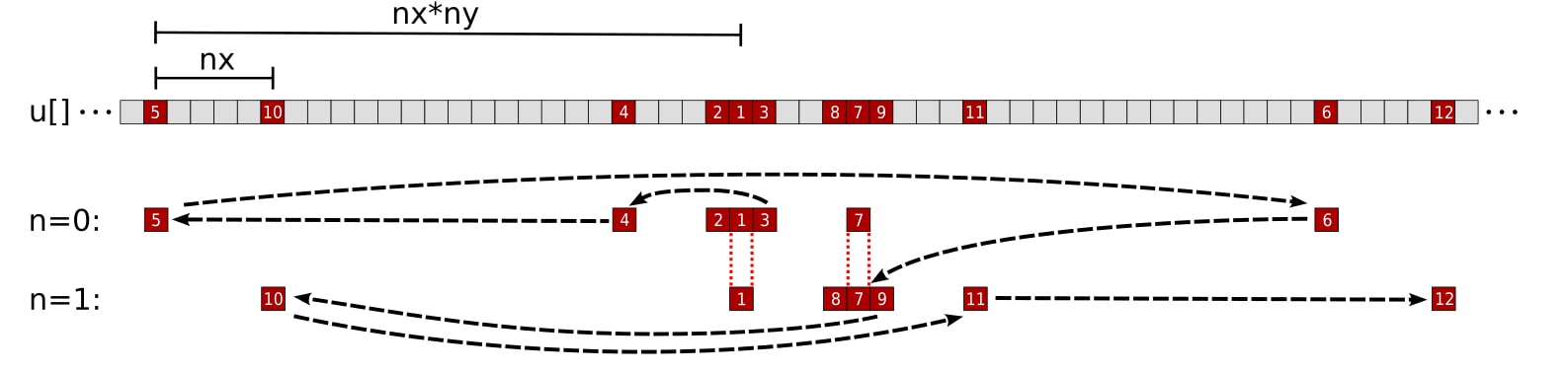
图 3:内核 2 中单个线程对于数组 `u` 的内存访问模式,块因子为 `m = 2`。数字和黑箭头对应于线程访问 `u` 元素 的顺序。`n = 0` 和 `n = 1` 行分别表示网格点 `pos` 和 `pos + nx` 的模板计算所需的 `u` 元素。第一个访问的元素(`u[pos]`)在 `n = 0` 迭代期间加载,并重用于 `n = 1` 迭代的 `y - 1` 元素。同样,第七个访问的元素(`u[pos + nx]`)在 `n = 1` 迭代期间加载,并重用于 `n = 0` 迭代的 `y + 1` 元素。
我们立刻发现了一个问题。线程经常需要在u数组的内存空间中“向后”跳转。在访问完每个网格点的z + 1元素后,线程需要“向后”跳转以访问n的下一次迭代的x方向元素。频繁地向前和向后访问u元素可能会过早地将可重用数据从缓存中驱逐出去。我们宁愿重新排序内核中的指令,只使用一个方向,即按升序地址访问内存。
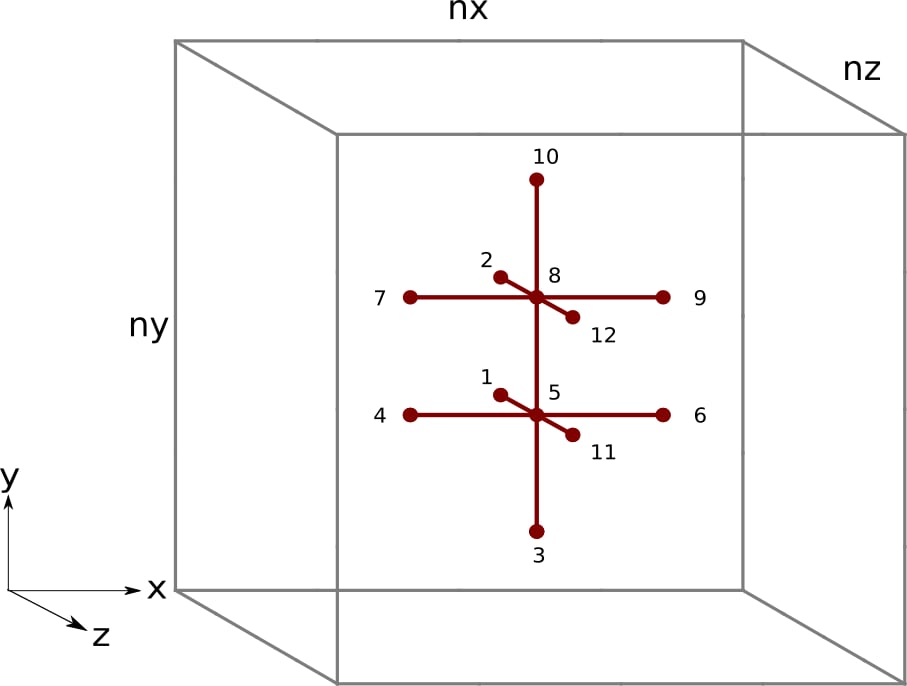
图 4:三维空间中的有限差分模板,块因子为m = 2。黑色的数字表示提出的内核中的每个线程访问u元素的顺序。
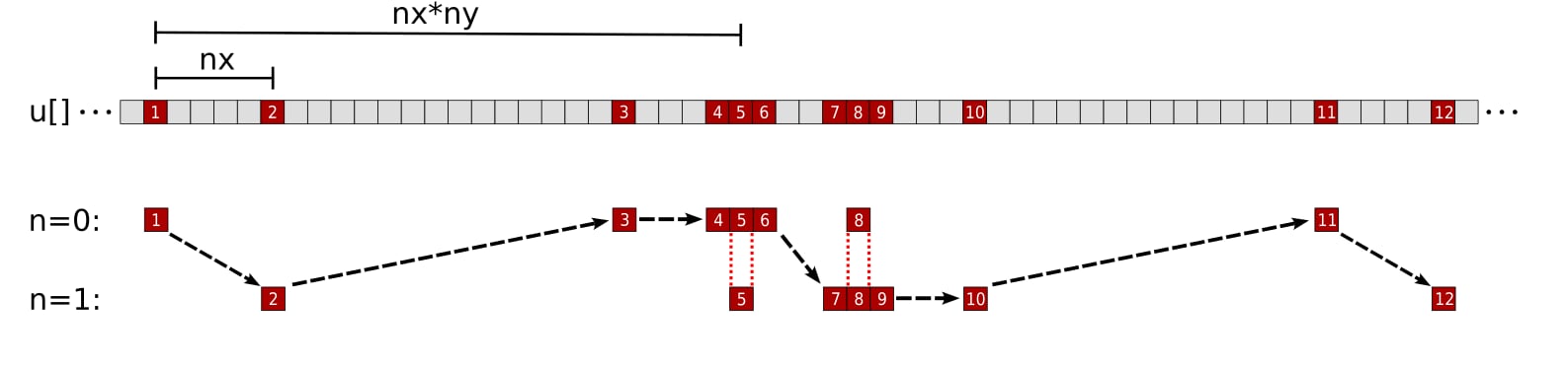
图 5:单个线程对数组u提出的内存访问模式,块因子为m = 2。数字和黑色箭头对应线程访问u元素的顺序。n = 0和n = 1行分别代表网格点pos和pos + nx的模板计算所需的u元素。第五个访问的元素(u[pos])在n = 0迭代期间加载,并在n = 1迭代的y - 1元素中重用。同样,第八个访问的元素(u[pos + nx])在n = 1迭代期间加载,并在n = 0迭代的y + 1元素中重用。
在这种不同的方法下,我们首先访问所有的z - 1元素,然后是迭代n = 0的y - 1元素,所有的x方向元素,迭代n = m - 1的y + 1元素,最后是所有的z + 1元素。现在每个线程都按升序内存地址访问所有需要的u元素。内核需要进行大幅重写,因此我们首先展示完整的实现。
// Tiling factor#define m 1template <typename T>__global__ void laplacian_kernel(T * f, const T * u, int nx, int ny, int nz, T invhx2, T invhy2, T invhz2, T invhxyz2) {
int i = threadIdx.x + blockIdx.x * blockDim.x; int j = m*(threadIdx.y + blockIdx.y * blockDim.y); int k = threadIdx.z + blockIdx.z * blockDim.z;
// Exit if this thread is on the xz boundary if (i == 0 || i >= nx - 1 || k == 0 || k >= nz - 1) return;
const int slice = nx * ny; size_t pos = i + nx * j + slice * k;
// Each thread accumulates m stencils in the y direction T Lu[m] = {0};
// Scalar for reusable data T center;
// z - 1, loop tiling for (int n = 0; n < m; n++) Lu[n] += u[pos - slice + n*nx] * invhz2;
// y - 1 Lu[0] += j > 0 ? u[pos - 1*nx] * invhy2 : 0; // bound check
// x direction, loop tiling for (int n = 0; n < m; n++) { // x - 1 Lu[n] += u[pos - 1 + n*nx] * invhx2;
// x center = u[pos + n*nx]; // store for reuse Lu[n] += center * invhxyz2;
// x + 1 Lu[n] += u[pos + 1 + n*nx] * invhx2;
// reuse: y + 1 for prev n if (n > 0) Lu[n-1] += center * invhy2;
// reuse: y - 1 for next n if (n < m - 1) Lu[n+1] += center * invhy2; }
// y + 1 Lu[m-1] += j < ny - m ? u[pos + m*nx] * invhy2 : 0; // bound check
// z + 1, loop tiling for (int n = 0; n < m; n++) Lu[n] += u[pos + slice + n*nx] * invhz2;
// Store only if thread is inside y boundary for (int n = 0; n < m; n++) if (n + j > 0 && n + j < ny - 1) f[pos + n*nx] = Lu[n];}
template <typename T>void laplacian(T *d_f, T *d_u, int nx, int ny, int nz, int BLK_X, int BLK_Y, int BLK_Z, T hx, T hy, T hz) {
dim3 block(BLK_X, BLK_Y, BLK_Z); dim3 grid((nx - 1) / block.x + 1, (ny - 1) / (block.y * m) + 1, (nz - 1) / block.z + 1); T invhx2 = (T)1./hx/hx; T invhy2 = (T)1./hy/hy; T invhz2 = (T)1./hz/hz; T invhxyz2 = -2. * (invhx2 + invhy2 + invhz2);
laplacian_kernel<<<grid, block>>>(d_f, d_u, nx, ny, nz, invhx2, invhy2, invhz2, invhxyz2);}现在我们来详细介绍内核中的计算步骤。首先,我们访问所有的z - 1网格点,然后是单个y - 1。
// z - 1, loop tiling for (int n = 0; n < m; n++) Lu[n] += u[pos - slice + n*nx] * invhz2;
// y - 1 Lu[0] += j > 0 ? u[pos - 1*nx] * invhy2 : 0; // bound check请注意,引入了条件运算符,以便它仅在n = 0网格点不位于y边界时才计算y - 1模板。在线程级别,既不重用z - 1也不重用y - 1元素。
接下来,线程计算x方向的模板。
// x direction, loop tiling for (int n = 0; n < m; n++) { // x - 1 Lu[n] += u[pos - 1 + n*nx] * invhx2;
// x center = u[pos + n*nx]; // store for reuse Lu[n] += center * invhxyz2;
// x + 1 Lu[n] += u[pos + 1 + n*nx] * invhx2;
// reuse: y + 1 for prev n if (n > 0) Lu[n-1] += center * invhy2;
// reuse: y - 1 for next n if (n < m - 1) Lu[n+1] += center * invhy2; }同样,在线程级别不重用x - 1或x + 1点,但中心元素u[pos + n*nx]可以像前一个内核一样重用最多两次。
之后,我们加载最后的y + 1点以及所有的z + 1点。
// y + 1 Lu[m-1] += j < ny - m ? u[pos + m*nx] * invhy2 : 0; // bound check
// z + 1, loop tiling for (int n = 0; n < m; n++) Lu[n] += u[pos + slice + n*nx] * invhz2;另一个条件运算符用于计算n = m - 1网格点的y + 1模板,前提是它不位于y边界。
最后,位于y边界内的所有线程都被写回内存。
// Store only if thread is inside y boundary for (int n = 0; n < m; n++) if (n + j > 0 && n + j < ny - 1) f[pos + n*nx] = Lu[n];现在我们尝试相同的块因子,看看这种重新排序是否会带来任何区别。
加速 | 目标值百分比 | |
|---|---|---|
内核 1 – 基线 | 1.00 | 69.4% |
内核 2 – 循环分块 m=1 | 1.00 | 69.4% |
内核 2 – 循环分块 m=2 | 0.98 | 68.3% |
内核 2 – 循环分块 m=4 | 0.94 | 65.5% |
内核 2 – 循环分块 m=8 | 0.92 | 64.0% |
内核 2 – 循环分块 m=16 | 0.29 | 20.1% |
内核 3 – 重新排序的加载 m=1 | 1.20 | 82.9% |
内核 3 – 重新排序的加载 m=2 | 1.28 | 88.9% |
内核 3 – 重新排序的加载 m=4 | 1.34 | 93.1% |
内核 3 – 重新排序的加载 m=8 | 1.37 | 94.8% |
内核 3 – 重新排序的加载 m=16 | 0.42 | 29.4% |
即使m=1,u元素的重新排序访问模式也已经提供了显著的性能提升。每个m的渐进式速度提升是我们预期的。让我们检查一下这个新内核的rocprof指标。
FETCH_SIZE (GB) | 获取效率 (%) | L2CacheHit (%) | |
|---|---|---|---|
理论值 | 1.074 | – | – |
内核 1 – 基线 | 2.014 | 53.3 | 65.0 |
内核 2 – 循环分块 m=1 | 2.014 | 53.3 | 65.0 |
内核 2 – 循环分块 m=2 | 1.848 | 58.1 | 60.5 |
内核 2 – 循环分块 m=4 | 1.880 | 57.1 | 57.0 |
内核 2 – 循环分块 m=8 | 1.820 | 59.0 | 56.0 |
内核 2 – 循环分块 m=16 | 5.637 | 19.1 | 40.9 |
内核 3 – 重新排序的加载 m=1 | 1.347 | 79.7 | 72.0 |
内核 3 – 重新排序的加载 m=2 | 1.166 | 92.1 | 70.6 |
内核 3 – 重新排序的加载 m=4 | 1.107 | 97.0 | 68.8 |
内核 3 – 重新排序的加载 m=8 | 1.080 | 99.4 | 67.7 |
内核 3 – 重新排序的加载 m=16 | 3.915 | 27.4 | 44.5 |
FETCH_SIZE指标显著下降,使我们非常接近理论极限。L2CacheHit率不仅提高,而且现在超过了我们最初从基线内核获得的水平。然而,我们注意到当m=16时,缓存命中率显著下降,同时获取大小显著增加。对于选定的问题,内核 3 配合 m=8是迄今为止最好的内核,达到了目标有效内存带宽的近 95%,获取效率超过 99%。
总结
结合这两种优化,FETCH_SIZE减少了高达 2 倍。这表明我们的 HIP 内核可以高效地为特定的网格大小加载数据。为了实现这一点,我们首先通过显式评估多个模板(通过循环分块)来减少每个存储指令的加载次数。然而,我们最初的实现并没有提高性能。为了解决这个问题,我们重新排序了内存访问模式以提高 L2 缓存命中率。现在的问题是,我们是否已经完成了对有限差分法求解拉普拉斯算子的初始 HIP 实现的优化。我们必须首先解决一些遗留问题。
-
还有进一步提高性能的空间吗?我们已经优化了 L2 缓存和全局内存之间的内存移动,因此我们必须在其他领域寻找性能提升,例如延迟隐藏。
-
为什么
m=16的性能会显著下降?无论是否重新排序内存访问,都会发生这种情况。也许解决潜在问题有助于我们更接近目标? -
其他架构和问题大小如何影响块因子的选择?我们迄今为止的所有优化都是针对单个 MI250X GCD 和问题大小
nx,ny,nz = 512, 512, 512量身定制的。
本系列的下一篇文章将回答其中一些待解决的问题。
如果您有任何问题或评论,请在 GitHub 讨论区 与我们联系
测试使用 ROCm 5.3.0-63 版本进行。基准测试结果不是经过验证的性能数据,仅用于展示代码修改的相对性能改进。实际性能结果取决于多种因素,包括系统配置和环境设置,不保证结果的可重现性。