使用 HIP 和 OpenMP 卸载的 Jacobi 求解器

最初发布于：
最后更新于：
Asitav Mishra's avatar
Asitav Mishra
通讯作者
Rajat Arora's avatar
Rajat Arora
作者
Justin Chang's avatar
Justin Chang
作者
Brian Cornille's avatar
Brian Cornille
审稿人
Mahdieh Ghazimirsaeed's avatar
Mahdieh Ghazimirsaeed
审稿人

Jacobi 方法是一种基本迭代线性求解器，用于求解偏微分方程（PDE），这些方程控制着高性能计算（HPC）应用中对多种物理现象感兴趣的方程。通过数值方法（例如有限差分、有限体积、有限元或其他方法）离散化 PDE，会得到一个大型稀疏方程组。像 Jacobi 这样的固定迭代方法可以利用现代异构分层系统（包括 CPU 和 GPU），因为它更易于并行化，并且与传统的直接方法相比，所需的内存更少。Jacobi 迭代涉及大量重复的矩阵-向量乘法运算，并且在很大程度上限制了每次迭代时所有组件之间的通信。这使得 Jacobi 方法更适合 GPU 卸载。

在这篇博文中，我们探讨了使用 HIP 和 OpenMP target 指令进行 GPU 卸载，并讨论了它们在实现工作量和性能方面的相对优势。

注意：虽然当今大多数 HPC 应用都使用消息传递接口（MPI）来实现分布式内存并行，但在本博文中，出于演示目的，我们仅考虑 Jacobi 方法的单进程实现。

Jacobi 迭代方法

为了讨论 Jacobi 迭代方法，我们考虑一个具有狄利克雷边界条件的二维区域上的 PDE，其空间坐标为 xx 和 yy，以求解泊松方程：−∇2u(x,y)=f-\nabla^2 u(x,y) = f。其中，u(x,y)u(x,y) 是区域内的光滑函数。方程使用有限差分方法[1] 在笛卡尔坐标系中用 5 点模板离散化

−ui−1,j+2ui,j−ui+1,jΔx2+−ui,j−1+2ui,j−ui,j+1Δy2=fi,j\frac{-u_{i-1,j } + 2u_{i,j} - u_{i+1,j }}{\Delta x^2} + \frac{-u_{i, j-1} + 2u_{i,j} - u_{i, j+1}}{\Delta y^2} = f_{i,j}

上述有限差分拉普拉斯算子导致了一个稀疏矩阵算子 AA 作用于未知向量 u\bf u：Au=fA {\bf u} = f。这里

u=[u1,1,u1,2,⋯ ,u2,1,⋯ ,ui,j,⋯uni,nj].{\bf u} = [u_{1,1}, u_{1,2}, \cdots, u_{2,1}, \cdots, u_{i,j}, \cdots u_{n_i,n_j}].

如果将矩阵分解为对角线部分（DD）、下三角部分（LL）和上三角部分（UU）（A=[D+L+U]A = [D + L + U]），Jacobi 迭代方法可以表示为

uk+1=uk+D−1(f−Auk){\bf u}^{k+1} = {\bf u}^{k} + D^{-1} \left( {\bf f} - A {\bf u}^k \right)

这里，kk 指的是迭代次数。 u(k=0){\bf u}^{(k=0)} 的值是初始条件。

Jacobi 代码结构

串行（CPU）Jacobi 求解器的主要组成部分是

  • 设置 Jacobi 对象

    • CreateMesh()
    • InitializeData()

  • 执行 Jacobi 方法

    • Laplacian()
    • BoundaryConditions()
    • Update()
    • Norm()

下面的代码展示了 Jacobi 求解器程序。在代码中，Jacobi_t Jacobi(mesh); 完成 Jacobi 对象的设置，而 Jacobi.Run() 完成 Jacobi 求解器的执行。

int main(int argc, char ** argv)
{
  mesh_t mesh;
  // Extract topology and domain dimensions from the command-line arguments
  ParseCommandLineArguments(argc, argv, mesh);
  Jacobi_t Jacobi(mesh);
  Jacobi.Run();
  return STATUS_OK;
}

设置 Jacobi 对象

Jacobi 对象由两个主要组成部分构成

  • 设置 Jacobi 对象

    • CreateMesh()
    • InitializeData()

例程 CreateMesh() 创建一个具有均匀网格间距的二维笛卡尔网格——参见图 1。例程 InitializeData() 初始化主机变量 u\bf u（代码中的 h_U）、矩阵向量乘积 AuA{\bf u}（h_AU）、右侧向量 ff（h_RHS）以及残差向量 f−Auf-A{\bf u}（h_RES）。它还对这些变量应用边界条件。

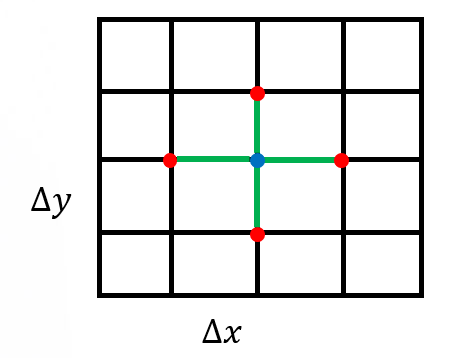
图 1：用于离散计算域的均匀矩形网格

执行 Jacobi 方法

Jacobi 求解器执行的主要内容包括以下函数

  • 执行 Jacobi 方法

    • Laplacian()
    • BoundaryConditions()
    • Update()
    • Norm()

下面的代码展示了每次 Jacobi 迭代中的函数调用顺序

// Scalar factor used in Jacobi method
const dfloat factor = 1/(2.0/(mesh.dx*mesh.dx) + 2.0/(mesh.dy*mesh.dy));
const dfloat _1bydx2 = 1.0/(mesh.dx*mesh.dx);
const dfloat _1bydy2 = 1.0/(mesh.dy*mesh.dy);


while ((iterations < JACOBI_MAX_LOOPS) && (residual > JACOBI_TOLERANCE))
{
  // Compute Laplacian
  Laplacian(mesh, _1bydx2, _1bydy2, h_U, h_AU);


  // Apply Boundary Conditions
  BoundaryConditions(mesh, _1bydx2, _1bydy2, h_U, h_AU);


  // Update the solution
  Update(mesh, factor, h_RHS, h_AU, h_RES, h_U);


  // Compute residual = ||U||
  residual = Norm(mesh, h_RES);


  ++iterations;
}

函数 Laplacian() 执行前面讨论的主要拉普拉斯运算，其代码如下

// AU_i,j = (-U_i+1,j + 2U_i,j - U_i-1,j)/dx^2 +
//          (-U_i,j+1 + 2U_i,j - U_i,j-1)/dy^2
void Laplacian(mesh_t& mesh,
               const dfloat _1bydx2,
               const dfloat _1bydx2,
               const dfloat * U,
               dfloat * AU) {
  int stride = mesh.Nx;
  int localNx = mesh.Nx - 2;
  int localNy = mesh.Ny - 2;


  for (int j=0;j<localNy;j++) {
    for (int i=0;i<localNx;i++) {


      const int id = (i+1) + (j+1)*stride;


      const int id_l = id - 1;
      const int id_r = id + 1;
      const int id_d = id - stride;
      const int id_u = id + stride;


      AU[id] = (-U[id_l] + 2*U[id] - U[id_r])/(dx*dx) +
               (-U[id_d] + 2*U[id] - U[id_u])/(dy*dy);
    }
  }
}

BoundaryConditions() 是一个用于对 AuA{\bf u} 项应用边界条件的函数。它仅应用于边界节点

void BoundaryConditions(mesh_t& mesh,
                        const dfloat _1bydx2,
                        const dfloat _1bydy2,
                        dfloat* U,
                        dfloat* AU) {


  const int Nx = mesh.Nx;
  const int Ny = mesh.Ny;


  for (int id=0;id<2*Nx+2*Ny-2;id++) {


    //get the (i,j) coordinates of node based on how large id is
    int i, j;
    if (id < Nx) { //bottom
      i = id;
      j = 0;
    } else if (id<2*Nx) { //top
      i = id - Nx;
      j = Ny-1;
    } else if (id < 2*Nx + Ny-1) { //left
      i = 0;
      j = id - 2*Nx + 1;
    } else { //right
      i = Nx-1;
      j = id - 2*Nx - Ny + 2;
    }


    const int iid = i+j*Nx;


    const dfloat U_d = (j==0)    ?  0.0 : U[iid - Nx];
    const dfloat U_u = (j==Ny-1) ?  0.0 : U[iid + Nx];
    const dfloat U_l = (i==0)    ?  0.0 : U[iid - 1];
    const dfloat U_r = (i==Nx-1) ?  0.0 : U[iid + 1];


     AU[iid] = (-U_l + 2*U[iid] - U_r)*_1bydx2 +
               (-U_d + 2*U[iid] - U_u)*_1bydy2;
  }
}

Jacobi 求解器的核心在于 Update() 函数，该函数执行 Jacobi 迭代

//Jacobi iterative method
// U = U + D^{-1}*(RHS - AU)
void Update(mesh_t& mesh,
            const dfloat factor,
            dfloat* RHS,
            dfloat* AU,
            dfloat* RES,
            dfloat* U)
{
  const int N = mesh.N;
  for (int id=0;id<N;id++)
  {
    const dfloat r_res = RHS[id] - AU[id];
    RES[id] = r_res;
    U[id] += r_res*factor;
  }
}

函数 Norm() 是执行归约运算并返回一个标量残差以检查求解器收敛性的主函数

dfloat Norm(mesh_t& mesh, dfloat *U) {
  dfloat norm = 0;
  const int N = mesh.N;
  const dfloat dx = mesh.dx;
  const dfloat dy = mesh.dy;
  for (int id=0; id < N; id++) {
    *norm2 += U[id] * U[id] * dx * dy;
  }
  return sqrt(norm)/N;
}

接下来的两个部分将描述将此求解器移植到 GPU 的两种可能方法。

使用 HIP 进行 GPU 卸载

首先，我们考虑使用 HIP 移植将 Jacobi 求解器卸载到 GPU。我们编写了 HIP 内核来移植上面讨论的四个主要代码区域。请注意，为了获得最优性能，我们将所有内核的启动边界设置为 256（BLOCK_SIZE）。下面的代码片段显示了每次 Jacobi 迭代中的函数调用，这与串行代码相同

// Scalar factor used in Jacobi method
const dfloat factor = 1/(2.0/(mesh.dx*mesh.dx) + 2.0/(mesh.dy*mesh.dy));
const dfloat _1bydx2 = 1.0/(mesh.dx*mesh.dx);
const dfloat _1bydy2 = 1.0/(mesh.dy*mesh.dy);


auto timerStart = std::chrono::high_resolution_clock::now();


while ((iterations < JACOBI_MAX_LOOPS) && (residual > JACOBI_TOLERANCE))
{
  // Compute Laplacian
  Laplacian(mesh, _1bydx2, _1bydy2, HD_U, HD_AU);


  // Apply Boundary Conditions
  BoundaryConditions(mesh, _1bydx2, _1bydy2, HD_U, HD_AU);


  // Update the solution
  Update(mesh, factor, HD_RHS, HD_AU, HD_RES, HD_U);


  // Compute residual = ||U||
  residual = Norm(mesh, HD_RES);


  ++iterations;
}

如以下代码片段所示，一些内核启动配置在 InitializeData() 中设置

// ...
  // Kernel launch configurations
  mesh.block.x = BLOCK_SIZE;
  mesh.grid.x = std::ceil(static_cast<double>(mesh.Nx * mesh.Ny) / mesh.block.x);
  mesh.grid2.x = std::ceil((2.0*mesh.Nx+2.0*mesh.Ny-2.0)/mesh.block.x);
// ...

下面显示了 LaplacianKernel() 和启动该内核的 Laplacian() 例程的代码

__global__
__launch_bounds__(BLOCK_SIZE)
void LaplacianKernel(const int localNx,
                     const int localNy,
                     const int stride,
                     const dfloat fac_dx2,
                     const dfloat fac_dy2,
                     const dfloat * U,
                     dfloat * AU)
{
    int tid = GET_GLOBAL_ID_0;


    if (tid > localNx + localNy * stride || tid < stride + 1)
        return;


    const int tid_l = tid - 1;
    const int tid_r = tid + 1;
    const int tid_d = tid - stride;
    const int tid_u = tid + stride;


    __builtin_nontemporal_store((-U[tid_l] + 2*U[tid] - U[tid_r])*fac_dx2 +
                                (-U[tid_d] + 2*U[tid] - U[tid_u])*fac_dy2, &(AU[tid]));
}


void Laplacian(mesh_t& mesh,
               const dfloat _1bydx2,
               const dfloat _1bydy2,
               dfloat* U,
               dfloat* AU)
{
  int stride = mesh.Nx;
  int localNx = mesh.Nx-2;
  int localNy = mesh.Ny-2;


  LaplacianKernel<<<mesh.grid,mesh.block>>>(localNx, localNy, stride, _1bydx2, _1bydy2, U, AU);
}

内核 BoundaryConditionsKernel() 及其启动函数如下所示

__global__
__launch_bounds__(BLOCK_SIZE)
void BoundaryConditionsKernel(const int Nx,
                              const int Ny,
                              const int stride,
                              const dfloat fac_dx2,
                              const dfloat fac_dy2,
                              const dfloat * U,
                              dfloat * AU)
{
  const int id = GET_GLOBAL_ID_0;


  if (id < 2*Nx+2*Ny-2)
  {
  //get the (i,j) coordinates of node based on how large id is
  int i = Nx-1;
  int j = id - 2*Nx - Ny + 2;


  if (id < Nx)
  { //bottom
      i = id; j = 0;
  }
  else if (id<2*Nx)
  { //top
    i = id - Nx; j = Ny-1;
  }
  else if (id < 2*Nx + Ny-1)
  { //left
    i = 0; j = id - 2*Nx + 1;
  }


  const int iid = i+j*stride;


  const dfloat U_d = (j==0)    ?  0.0 : U[iid - stride];
  const dfloat U_u = (j==Ny-1) ?  0.0 : U[iid + stride];
  const dfloat U_l = (i==0)    ?  0.0 : U[iid - 1];
  const dfloat U_r = (i==Nx-1) ?  0.0 : U[iid + 1];


  __builtin_nontemporal_store((-U_l + 2*U[iid] - U_r)*fac_dx2 +
                                    (-U_d + 2*U[iid] - U_u)*fac_dy2, &(AU[iid]));
  }
}


void BoundaryConditions(mesh_t& mesh,
                        const dfloat _1bydx2,
                        const dfloat _1bydy2,
                        dfloat* U,
                        dfloat* AU) {


  const int Nx = mesh.Nx;
  const int Ny = mesh.Ny;
  BoundaryConditionsKernel<<<mesh.grid2,mesh.block>>>(Nx, Ny, Nx, _1bydx2, _1bydy2, U, AU);
}

下面的代码展示了 UpdateKernel() 的 HIP 实现

__global__
__launch_bounds__(BLOCK_SIZE)
void UpdateKernel(const int N,
                  const dfloat factor,
                  const dfloat *__restrict__ RHS,
                  const dfloat *__restrict__ AU,
                  dfloat *__restrict__ RES,
                  dfloat *__restrict__ U)
{
  int tid = GET_GLOBAL_ID_0;
  dfloat r_res;
  for (int i = tid; i < N; i += gridDim.x * blockDim.x)
  {
    r_res = RHS[i] - AU[i];
    RES[i] = r_res;
    U[i] += r_res*factor;
  }
}


void Update(mesh_t& mesh,
            const dfloat factor,
            dfloat* RHS,
            dfloat* AU,
            dfloat* RES,
            dfloat* U)
{
  UpdateKernel<<<mesh.grid,mesh.block>>>(mesh.N, factor, RHS, AU, RES, U);
}

下面的代码展示了 NormKernel() 的 HIP 实现，该实现松散地基于 BabelStream 中的 HIP dot 实现

#define NORM_BLOCK_SIZE 512
#define NORM_NUM_BLOCKS 256
__global__
__launch_bounds__(NORM_BLOCK_SIZE)
void NormKernel(const dfloat * a, dfloat * sum, int N)
{
  __shared__ dfloat smem[NORM_BLOCK_SIZE];


  int i = GET_GLOBAL_ID_0;
  const size_t si = GET_LOCAL_ID_0;


  smem[si] = 0.0;
  for (; i < N; i += NORM_BLOCK_SIZE * NORM_NUM_BLOCKS)
    smem[si] += a[i] * a[i];


  for (int offset = NORM_BLOCK_SIZE >> 1; offset > 0; offset >>= 1)
  {
    __syncthreads();
    if (si < offset) smem[si] += smem[si+offset];
  }


  if (si == 0)
    sum[GET_BLOCK_ID_0] = smem[si];
}


void NormSumMalloc(mesh_t &mesh)
{
  hipHostMalloc(&mesh.norm_sum, NORM_NUM_BLOCKS*sizeof(dfloat), hipHostMallocNonCoherent);
}


dfloat Norm(mesh_t& mesh, dfloat *U)
{
  dfloat norm = 0.0;
  const int N = mesh.N;
  const dfloat dx = mesh.dx;
  const dfloat dy = mesh.dy;
  NormKernel<<<NORM_NUM_BLOCKS,NORM_BLOCK_SIZE>>>(U, mesh.norm_sum, N);
  hipDeviceSynchronize();
  for (int id=0; id < NORM_NUM_BLOCKS; id++)
    norm += mesh.norm_sum[id];
  return sqrt(norm*dx*dy)*mesh.invNtotal;
}

请注意，缓冲区 mesh.norm_sum 是非一致性固定内存，这意味着它被映射到 GPU 的地址空间。我们建议所有感兴趣的读者参考这篇文章以获得更全面的讨论。参数 NORM_BLOCK_SIZE 和 NORM_NUM_BLOCKS 可以并且应该进行调整，以优化硬件性能。

下表总结了带有 HIP 移植的 Jacobi 求解器主要内核的每次迭代时间。网格大小为 4096×40964096\times 4096。在 MI250 GPU 的一个 GCD 上，进行 1000 次迭代的总挂钟时间为 858 毫秒，计算性能为 332 GFLOP/s。开销最大的代码区域是 Jacobi Update() 例程。

内核

平均时间（毫秒）

百分比

Update

0.51

60.9

Laplacian

0.22

25.7

Norm

0.10

12.3

BoundaryConditions

0.01

0.9

使用 OpenMP 进行 GPU 卸载

在本节中，我们探讨 OpenMP 卸载。我们考虑结构化和非结构化目标数据映射方法。使用 clang++ 编译器和 -fopenmp 标志来构建 openmp 目标卸载区域。更多详细信息可以在 codes/Makefile 中找到。例如，下面的命令展示了如何编译 Jacobi.cpp 文件

终端窗口
/opt/rocm/llvm/bin/clang++ -Ofast -g -fopenmp --offload-arch=gfx90a -c Jacobi.cpp -o Jacobi.o

结构化目标数据映射

让我们考虑 HIP 移植的 Jacobi 求解器中开销最大的代码区域 Update()。一种简单的 OpenMP 目标卸载方法如下所示

void Update(mesh_t& mesh,
            const dfloat factor,
            dfloat* RHS,
            dfloat* AU,
            dfloat* RES,
            dfloat* U)
{
  const int N = mesh.N;
  #pragma omp target data map(to:RHS[0:N],AU[0:N]) map(from:RES[0:N]) map(tofrom:U[0:N])
  #pragma omp target teams distribute parallel for
  for (int id=0;id<N;id++)
  {
    const dfloat r_res = RHS[id] - AU[id];
    RES[id] = r_res;
    U[id] += r_res*factor;
  }
}

状态变量被映射到设备区域，Jacobi 更新在目标区域中调用。这是结构化目标映射构造的一个例子。类似地，Laplacian 和 Norm 例程也进行了结构化目标映射。

void Laplacian(mesh_t& mesh,
               const dfloat _1bydx2,
               const dfloat _1bydy2,
               dfloat* U,
               dfloat* AU)
{
  int stride = mesh.Nx;
  int localNx = mesh.Nx-2;
  int localNy = mesh.Ny-2;


  #pragma omp target data map(to:U[0:mesh.N]) map(tofrom:AU[0:mesh.N])
  #pragma omp target teams distribute parallel for collapse(2)
  for (int j=0;j<localNy;j++) {
    for (int i=0;i<localNx;i++) {


      const int id = (i+1) + (j+1)*stride;


      const int id_l = id - 1;
      const int id_r = id + 1;
      const int id_d = id - stride;
      const int id_u = id + stride;


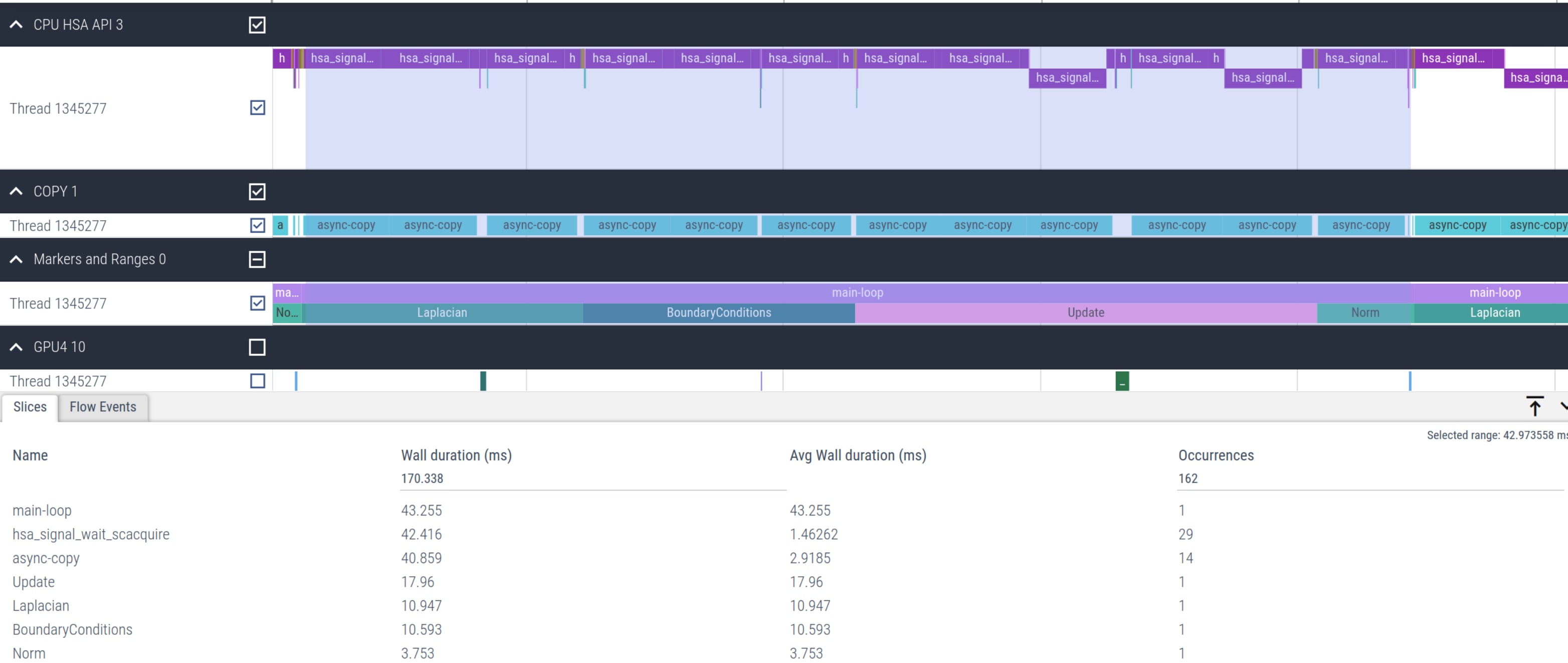
       AU[id] = (-U[id_l] + 2*U[id] - U[id_r])*_1bydx2 +
                (-U[id_d] + 2*U[id] - U[id_u])*_1bydy2;
    }
  }
}
dfloat Norm(mesh_t& mesh, dfloat *U)
{
  dfloat norm = 0.0;
  const int N = mesh.N;
  const dfloat dx = mesh.dx;
  const dfloat dy = mesh.dy;
  #pragma omp target data map(to: U[0:mesh.N])
  #pragma omp target teams distribute parallel for reduction(+:norm)
  for (int id=0; id < N; id++) {
    norm += U[id] * U[id] * dx * dy;
  }
  return sqrt(norm)/N;
}

然而，这种实现导致求解器性能非常差，每次主循环迭代需要 51.4 毫秒，而不是使用 HIP 的 1.1 毫秒。这大约慢了 46 倍。查看图 2，我们发现由于每次迭代都需要映射，因此在 hsa_signal_wait_scacquire 和特别是 async-copy 内核上花费了大量时间。

图 2：使用结构化目标数据映射的 Jacobi 卸载内核时间线

非结构化目标数据映射

我们注意到，Jacobi 求解器所需的大部分状态变量都可以驻留在设备上。数据仅在需要最终残差输出和状态解数据时才需要映射到主机（CPU）。因此，我们可以切换到非结构化目标数据映射构造，该构造确保数据在 target enter data 和 target exit data 映射构造之间驻留在设备上。我们通过在 Jacobi 迭代之前执行主机到设备复制，并在循环结束后释放设备数据，如下所示

void Jacobi_t::Run()
{
  const int N = mesh.N;
  #pragma omp target enter data map(to: mesh,h_U[0:N],h_AU[0:N],h_RES[0:N],h_RHS[0:N])
  ...
  while ((iterations < JACOBI_MAX_LOOPS) && (residual > JACOBI_TOLERANCE))
  {
    Laplacian(mesh, _1bydx2, _1bydy2, HD_U, HD_AU);
    BoundaryConditions(mesh, _1bydx2, _1bydy2, HD_U, HD_AU);
    Update(mesh, factor, HD_RHS, HD_AU, HD_RES, HD_U);
    residual = Norm(mesh, HD_RES);


    ++iterations;
  }
  ...
  #pragma omp target exit data map(release: h_U[0:N],h_AU[0:N],h_RES[0:N],h_RHS[0:N])
}

这避免了在每次迭代中重复进行主机到设备和设备到主机的映射，而这是结构化目标数据映射构造对所有例程（Laplacian、BoundaryConditions、Update 和 Norm）所必需的。这实际上意味着从这些例程中删除 #pragma omp target data map() 构造。

例如，下面的代码显示了现在更新的 Norm 函数在目标区域中不再有结构化映射构造。这里，状态向量 UU 已经使用非结构化数据映射构造在 Jacobi 求解器开始时映射到了设备上。

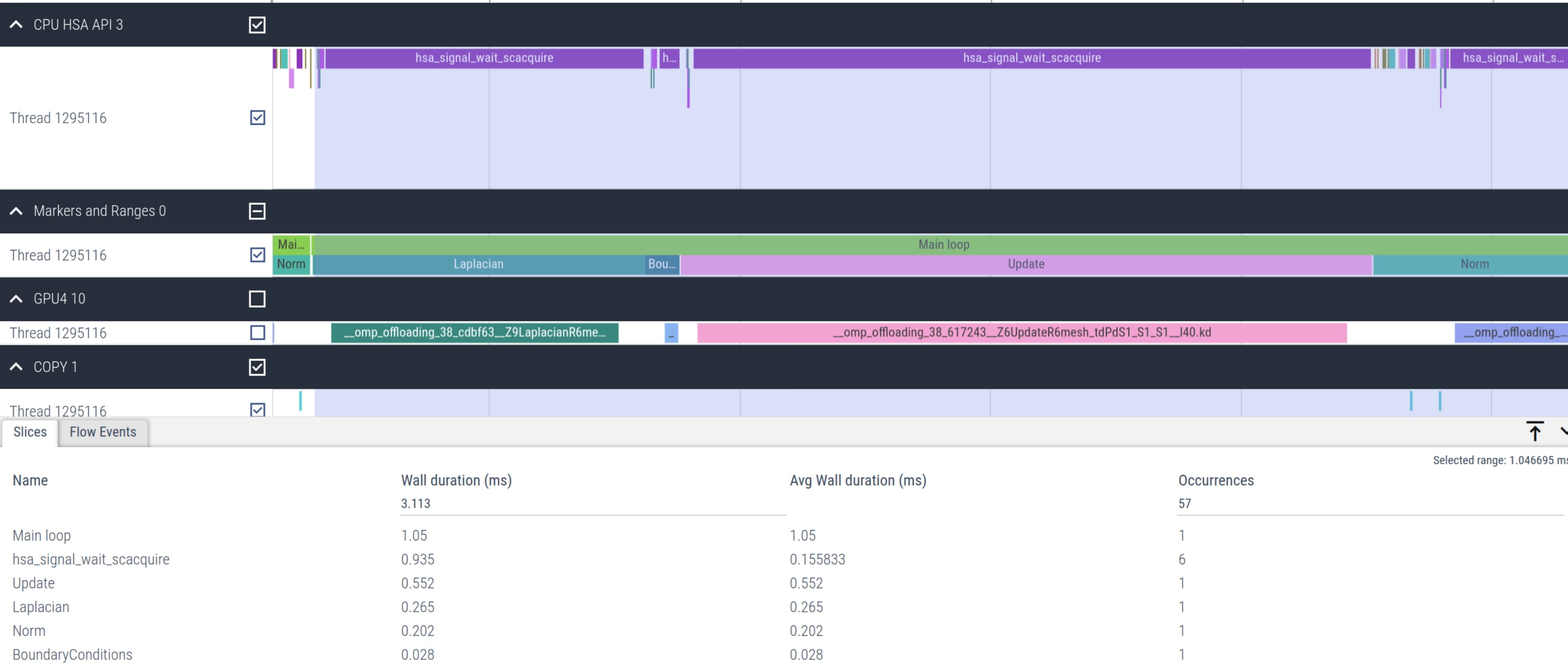
dfloat Norm(mesh_t& mesh, dfloat *U)
{
  dfloat norm = 0.0;
  const int N = mesh.N;
  const dfloat dx = mesh.dx;
  const dfloat dy = mesh.dy;
  #pragma omp target teams distribute parallel for reduction(+:norm)
  for (int id=0; id < N; id++) {
    norm += U[id] * U[id] * dx * dy;
  }
  return sqrt(norm)/N;
}

下面的图 3 显示了主要 Jacobi 求解器内核的时间线。该图清楚地表明，与图 2 中第一个朴素卸载实现观察到的相比，hsa_signal_wait_scacquire 内核调用的总数已大大减少。

图 3：使用非结构化映射的优化 Jacobi 卸载内核时间线

下表总结了使用 Clang 编译器通过 OpenMP 卸载实现的 Jacobi 求解器主要内核的时间。网格大小为 4096×40964096 \times 4096，与 HIP 版本一致。在 MI250 GPU 的一个 GCD 上，一千次迭代的总挂钟时间为 999 毫秒[2]，与之前观察到的 HIP 实现值非常接近。285 GFLOPs 的计算性能也与 HIP 实现值相当。总体而言，OpenMP 卸载的主要代码区域的时间与 HIP 移植获得的值非常接近。

内核

平均时间（毫秒）

百分比

Update

0.51

57.9

Laplacian

0.25

27.6

Norm

0.11

12.2

BoundaryConditions

0.02

2.2

HIP 与 OpenMP 卸载

具有稀疏矩阵运算的 Jacobi 求解器，其算术强度（AI = FLOPs/Band Width）约为 0.17，处于内存限制区域。因此，我们比较了 HIP 和 OpenMP 卸载实现中内核实现的内存带宽（BW）。下表比较了 HIP 和 OpenMP 卸载实现的 HBM BW（GB/s）值。

内核

HIP HBM BW (GB/s)

OpenMP 卸载 HBM BW (GB/s)

Update

1306

1297

Laplacian

1240

1091

Norm

1325

1239

BoundaryConditions

151

50

大多数内核实现的 BW 值非常接近 MI250 的理论峰值 BW（约 [1300-1400] GB/s）。BoundaryConditions 中的工作量太小，无法使 GPU 饱和，因此其值很小。下面图 4 显示了 Update 内核 HIP 和 OpenMP 卸载实现的屋顶线[3]。从屋顶线图可以看出，两个实现中的 Update 内核都非常接近内存限制区域的屋顶线。这与上面 HBM 表的观察结果非常吻合。

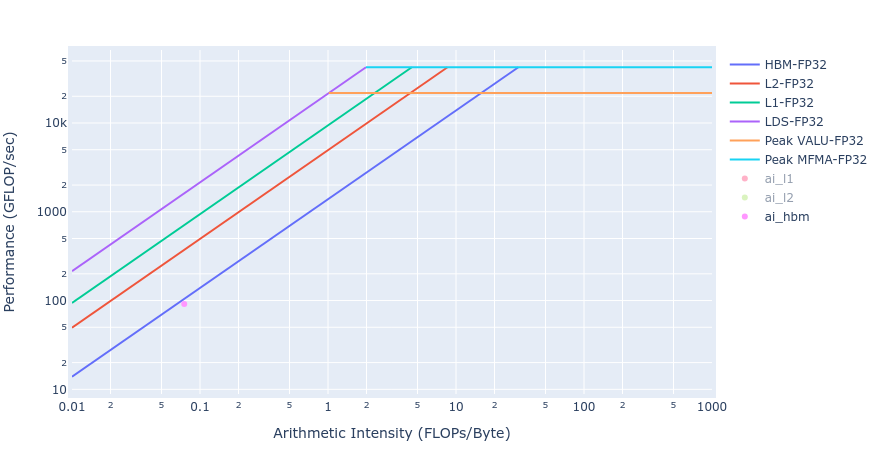
Light         Dark

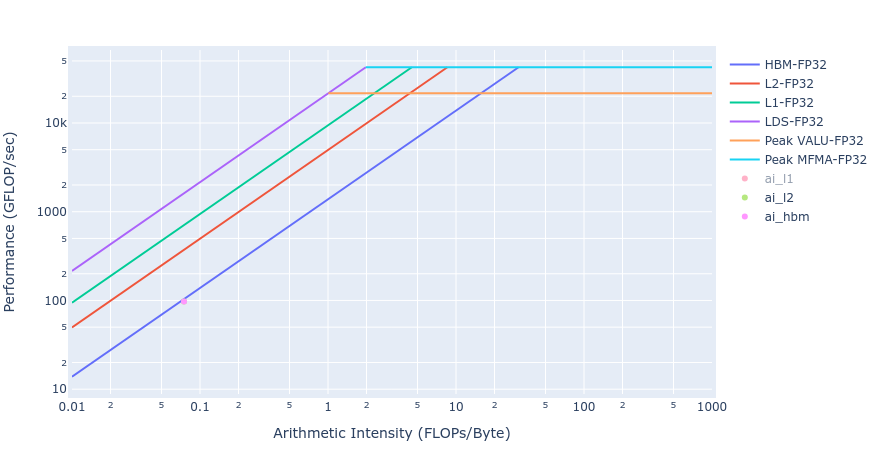
图 4：使用 HIP（左）和 OpenMP 卸载（右）的 Update 内核的屋顶线

从下面图 5 中两个 GPU 卸载实现的屋顶线可以得出关于 Laplacian 内核实现的 BW 的类似观察。

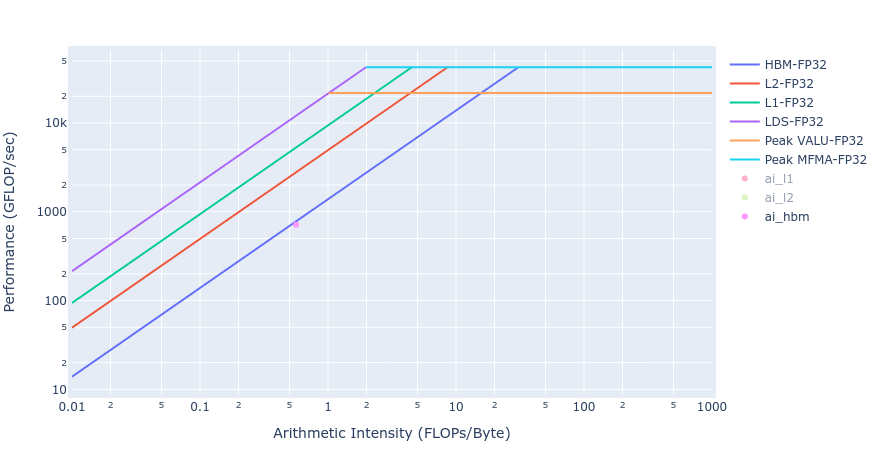
Light         Dark

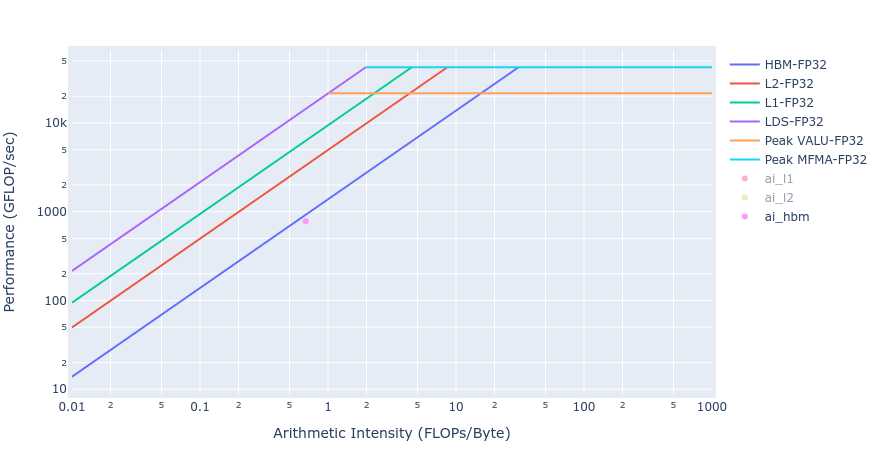
图 5：使用 HIP（左）和 OpenMP 卸载（右）的 Laplacian 内核的屋顶线

结论

在这篇博文中，我们介绍了使用 HIP 和 OpenMP 目标卸载的有限差分 Jacobi 求解器的 GPU 卸载。HIP 实现需要用新的 HIP 内核替换主机代码，并优化内核启动参数，包括线程块和网格大小以及启动边界。另一方面，基于指令的 OpenMP 卸载实现对现有主机代码库的修改侵入性较小。对于所考虑的问题规模，OpenMP 卸载能够实现与 HIP GPU 移植相当，甚至有时更好的计算性能和带宽指标，而编码工作量却大大减少。这说明了像 OpenMP 卸载这样的基于指令的 GPU 移植相对于 HIP 移植等涉及代码重写的代码所具有的优势。尽管如此，值得一提的是，对于更复杂的应用程序，OpenMP 可能只能提供有限的选项来调整目标卸载构造及其参数以获得额外的性能增益。

将来，我们将在这篇博文之后发布 Jacobi 求解器的 Fortran OpenMP 卸载版本。

[1]

请参阅有限差分博文。

[2]

结果使用 ROCM v.5.6.0-67 获得。这些数字未经验证，仅用于演示代码修改带来的相对性能提升。实际性能结果将取决于多种因素，包括系统配置和环境设置。

[3]

屋顶线使用 AMD Omniperf 工具获得。

Asitav Mishra's avatar

Asitav Mishra

通讯作者
Asitav Mishra 是 AMD 的高级技术员，专注于在现代 AMD GPU 上移植和优化科学应用程序，这些 GPU 驱动着世界上最大的超级计算机和埃克斯级超级计算机。他拥有马里兰大学航空航天工程博士学位。在加入 AMD 之前，他曾是美国国家航空航天局（National Institute of Aerospace）的高级研究工程师，支持 NASA 在计算空气动力学方面的项目。此外，他还在多所大学担任研究科学家和博士后职位，解决了复杂的跨学科航空航天问题。他的研究兴趣包括非稳态伴随方法、计算流体动力学（CFD）以及利用多种并行模型（包括 HIP/MPI/OpenMP/OpenACC）的高性能计算。
Rajat Arora's avatar

Rajat Arora

作者
Rajat Arora 是 AMD 数据中心 GPU 软件解决方案部门的高级技术人员 (SMTS) 软件系统设计工程师，他致力于为 AMD GPU 移植和优化高性能计算应用程序。他获得了卡内基梅隆大学计算力学博士学位。他的博士研究集中在高​​性能科学计算、数值分析和材料科学的交叉领域。最近，他的研究兴趣已扩展到包括物理信息机器学习模型的开发以及加速科学发现和工程设计的工具。
Justin Chang's avatar

Justin Chang

作者
Justin Chang 是 AMD 数据中心 GPU 软件解决方案部门的高级技术人员 (SMTS) 软件系统设计工程师，负责管理 AMD lab notes 博文系列。他获得了休斯顿大学土木工程博士学位，并发表了多篇关于多孔介质传输的结构保持高性能计算方法的期刊论文。作为博士后，他曾在莱斯大学和美国国家可再生能源实验室工作，以加速电动汽车所用双孔隙多孔介质和锂离子电池的地下流体模拟时间。他还曾在石油和天然气行业工作，专注于关键 FWI、RTM 和其他地震成像工作负载的 GPU 移植和优化。
Brian Cornille's avatar

Brian Cornille

审稿人
Brian Cornille 是 AMD 数据中心 GPU 软件解决方案组的技术员。他专注于支持面向 AMD GPU 的 Fortran 和 OpenMP 应用程序。他是 DOE 计算科学研究生奖学金的毕业生，拥有威斯康星大学麦迪逊分校核工程与工程物理学博士学位。他的博士研究课题是用于聚变能源应用的等离子体物理学的计算方法和分析。
Mahdieh Ghazimirsaeed's avatar

Mahdieh Ghazimirsaeed

审稿人
Mahdieh Ghazimirsaeed 是数据中心 GPU 软件解决方案部门的技术人员 (MTS) 软件系统设计工程师，负责优化 AMD 硬件的科学代码。她获得了加拿大皇后大学计算机工程博士学位，并发表了多篇关于通信库开发的论文。在加入 AMD 之前，她是俄亥俄州立大学的博士后研究员，从事 MVAPICH2 软件软件包的设计和开发。Mahdieh 的研究兴趣包括 HPC、异构和加速计算以及机器学习。

相关软件

相关新闻和技术文章

© . This site is unofficial and not affiliated with AMD.