有限差分法 – 拉普拉斯算子 第 4 部分

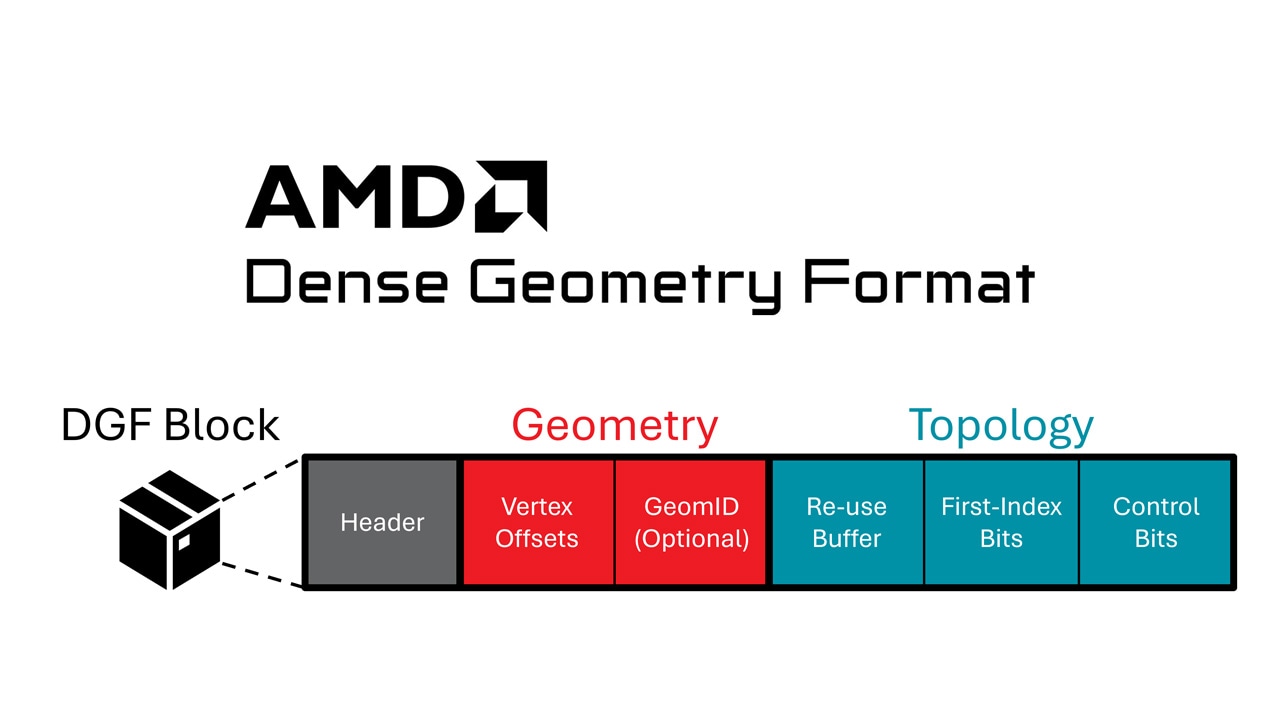
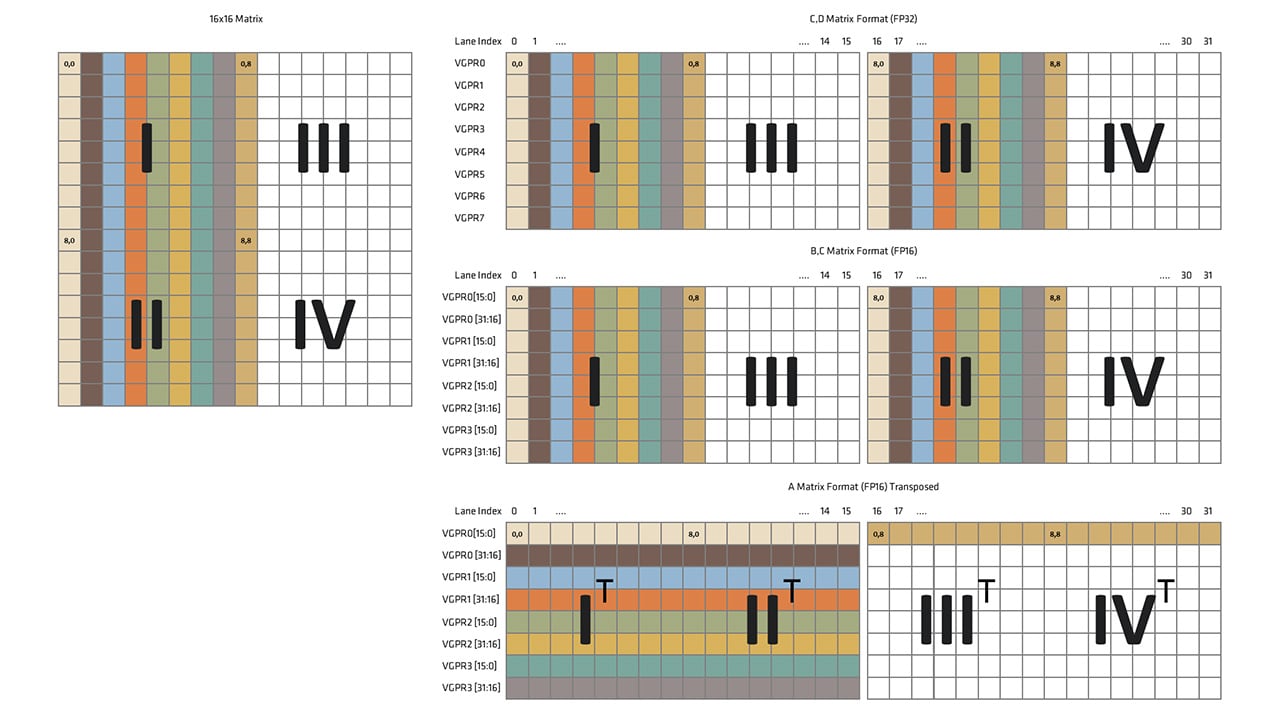
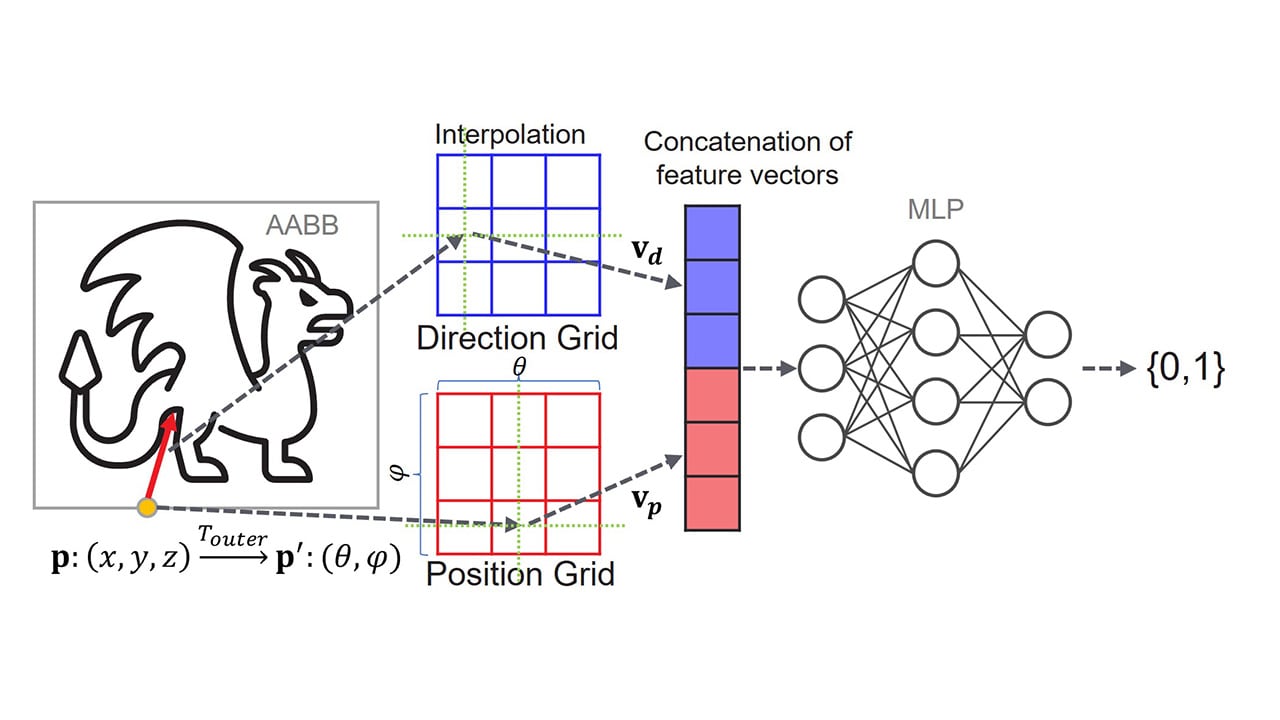
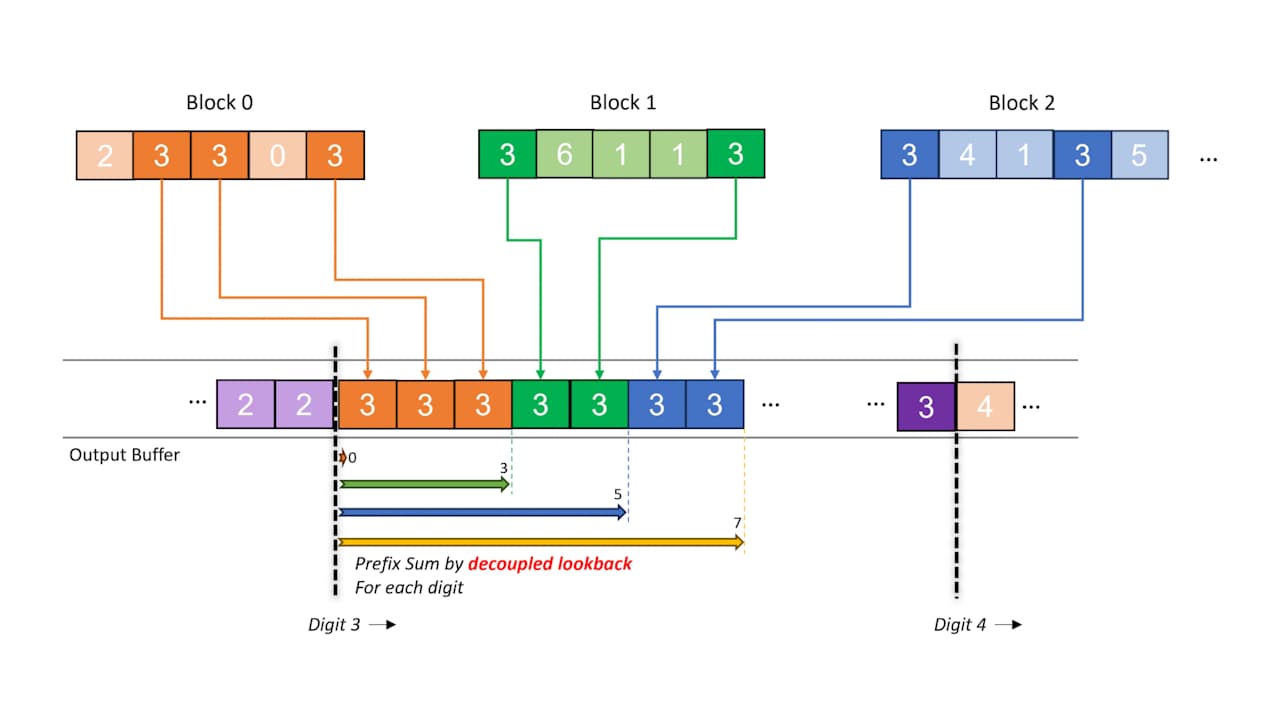
在前三篇文章中，我们介绍了用于拉普拉斯算子的有限差分法的 HIP 实现，并应用了四种不同的优化。在这些代码修改过程中，由于全局内存的读取次数减少，我们观察到了性能的逐步提升。然后，我们进一步优化以达到单块 MI250X GPU 上 512 $\times$ 512 $\times$ 512 网格点的预期性能目标。下面显示的是我们称之为 Kernel 5 的最终 HIP 内核。

// Tiling factor
#define m 8
// Launch bounds
#define LB 256
template <typename T>
__launch_bounds__(LB)
__global__ void laplacian_kernel(T * f, const T * u, int nx, int ny, int nz, T invhx2, T invhy2, T invhz2, T invhxyz2) {

    int i = threadIdx.x + blockIdx.x * blockDim.x;
    int j = m*(threadIdx.y + blockIdx.y * blockDim.y);
    int k = threadIdx.z + blockIdx.z * blockDim.z;

    // Exit if this thread is on the xz boundary
    if (i == 0 || i >= nx - 1 ||
        k == 0 || k >= nz - 1)
        return;

    const int slice = nx * ny;
    size_t pos = i + nx * j + slice * k;

    // Each thread accumulates m stencils in the y direction
    T Lu[m] = {0};

    // Scalar for reusable data
    T center;

    // z - 1, loop tiling
    for (int n = 0; n < m; n++)
        Lu[n] += u[pos - slice + n*nx] * invhz2;

    // y - 1
    Lu[0]   += j > 0 ? u[pos - 1*nx] * invhy2 : 0; // bound check

    // x direction, loop tiling
    for (int n = 0; n < m; n++) {
        // x - 1
        Lu[n] += u[pos - 1 + n*nx] * invhx2;

        // x
        center = u[pos + n*nx]; // store for reuse
        Lu[n] += center * invhxyz2;

        // x + 1
        Lu[n] += u[pos + 1 + n*nx] * invhx2;

        // reuse: y + 1 for prev n
        if (n > 0) Lu[n-1] += center * invhy2;

        // reuse: y - 1 for next n
        if (n < m - 1) Lu[n+1] += center * invhy2;
    }

    // y + 1
    Lu[m-1]  += j < ny - m ? u[pos + m*nx] * invhy2 : 0; // bound check

    // z + 1, loop tiling
    for (int n = 0; n < m; n++)
      Lu[n] += u[pos + slice + n*nx] * invhz2;

    // Store only if thread is inside y boundary
    for (int n = 0; n < m; n++)
      if (n + j > 0 && n + j < ny - 1)
        __builtin_nontemporal_store(Lu[n],&f[pos + n*nx]);
}

}

第 4 部分的目标是探讨该代码在各种 AMD GPU 和问题规模下所达到的性能。作为本次调查的一部分，我们将通过从经验中吸取的教训来结束拉普拉斯算子系列，并提供用户可以应用于类似问题的潜在代码优化。本文的其余部分概述如下：

1. 跨多种 AMD GPU 运行 Kernel 5，测试各种问题规模

2. 检查 L2 缓存命中性能并确定其性能下降的根本原因

3. 提出绕过 L2 缓存大小限制的技术

4. 回顾本拉普拉斯算子系列中进行的所有代码优化。

不同硬件和尺寸下的性能

除了 MI250X GPU 之外，还考虑了以下 AMD GPU：

1. RX 6900 XT

2. RX 7900 XTX

3. MI50

4. MI100

5. MI210

6. MI250

我们将对 Kernel 5 进行扩展研究，从所有上述 GPU 的问题规模 nx,ny,nz = 256, 256, 256 开始。每个维度都以 256 的倍数增加，直到达到 nx,ny,nz = 1024, 1024, 1024 的全局问题规模。回想一下，评价指标 (FOM) 定义为有效内存带宽

theoretical_fetch_size = ((nx * ny * nz - 8 - 4 * (nx - 2) - 4 * (ny - 2) - 4 * (nz - 2) ) * sizeof(double);
theoretical_write_size = ((nx - 2) * (ny - 2) * (nz - 2)) * sizeof(double);
effective_memory_bandwidth = (theoretical_fetch_size + theoretical_write_size) / average_kernel_execution_time;

这是数据传输的平均速率，考虑了需要穿过整个内存子系统的数据量。这里的目标是获得一个尽可能接近设备可实现的 HBM 带宽的 FOM。通过先前运行 Kernel 5 在各种线程块大小、启动边界和分块因子下的实验，我们发现以下参数在 512 $\times$ 512 $\times$ 512 点网格上为每个 GPU 提供了最高的 FOM：

从现在开始，将在单个 GCD 上对 MI250 和 MI250X GPU 进行实验。下图描绘了不同 AMD GPU 和问题规模下的 FOM[1]。

图 1：Kernel 5 在各种 AMD GPU 和问题规模下的性能

请注意，RX 6900 XT GPU 的内存不足以执行最大的示例 nx,ny,nz = 1024, 1924, 1024，因此它未显示在上图中。所有尺寸下 RX 6900 XT 和 RX 7900 XTX GPU 的性能似乎相对一致，而所有 Instinct™ GPU 在问题规模跨越特定阈值时性能都会下降。在接下来的部分中，我们将调查 Instinct™ GPU 性能下降的来源。

性能下降的根本原因

让我们将注意力重新回到 MI250X GPU。为了理解性能下降的原因，我们需要收集 rocprof 统计数据。我们首先收集 FETCH_SIZE 并将其与每个 nx,ny,nz 组合的 theoretical_fetch_size 进行比较。理想情况下，FETCH_SIZE 应等同于理论量，因为每个线程加载的元素最多可被相邻线程重用六次。值得注意的是，MI100、MI210、MI250 和 MI250X GPU 的 L2 缓存均为 8 MB，在每个 GCD 的计算单元 (CU) 之间共享，因此我们收集的 L2CacheHit 对于确定缓存数据重用程度非常有用。下图展示了我们在相同问题规模范围内的发现。

图 2：Kernel 5 在各种问题规模下，在单个 MI250X GCD 上的提取效率和 L2 缓存命中率

FOM、提取效率和 L2 缓存命中率之间存在明显的相关性。回想一下，在拉普拉斯算子第 1 部分的文章中，基线 HIP 内核的提取效率为 50%，同时保持相对较高的 L2 缓存命中率（65%）。这让我们认为内核设计存在问题。在最后一个实验中，提取效率和 L2 缓存命中率都稳定在 33% 左右，这表明性能的限制因素是 L2 缓存的大小。

上述图中的另一个有趣观察是，性能的下降仅发生在 nx 或 ny 增加时——nz 的增加对性能几乎没有影响。从 Kernel 5 中的线程块配置和网格索引可以看出，在获取下一个 xy 平面的元素之前，将从全局内存中获取单个 xy 平面的所有元素。每个线程的模板计算在 z 方向上的步幅为 -nx*ny、0 和 nx*ny，因此需要三个数据 xy 平面。如果这三个 xy 平面太大而无法同时放入 L2 缓存，那么每个线程将循环缓存以从全局内存中提取额外的 xy 平面——例如，当只有一个 xy 平面适合（或部分适合）L2 缓存时，线程需要从全局内存中循环两个额外的 xy 平面，因此提取效率会降至 33%。

让我们进行第二次实验来进一步说明这一点。我们将检查 nx 和 ny 的各种值，以确定性能开始下降之前的最佳 z 方向步幅。从大约 1 MB 的起始 z 步幅（相当于 nx,ny = 512,256）开始，并保持 nx 固定为三个不同的大小，我们逐渐增加 ny，直到 xy 平面超过 8 MB（nxnysizeof(double)）。见下图：

图 3：在单个 MI250X GCD 上，固定 nx 的各种值下，增加 nx*ny 步幅对性能的影响

无论 nx 的大小如何，当单个 xy 平面超过约 2.5 MB 内存时，性能都会下降。事实证明，2.5 MB 足以在 8 MB L2 缓存中容纳三个连续的 xy 平面，这解释了为什么 FOM 值更高。然而，步幅越大，从缓存中掉出的元素越多，从而降低了 L2CacheHit 率，进而降低了 FOM。当 nx*ny 超过 8 MB 时，性能会趋于稳定，因为此时只有一个平面适合（或部分适合）缓存——这时 FETCH_SIZE 是理论估计的三倍。

关于 Radeon™ GPU 性能的说明

有人可能会问，为什么 RX 6900 XT 和 RX 7900 XTX GPU 在图 1 所示的扩展研究中似乎不受影响。与 Instinct™ GPU 不同，Instinct™ GPU 的 L2 缓存是所有 CU 共享的最后一个缓存，即“最后一级缓存”（LLC），Radeon™ GPU 还有一个额外的共享缓存级别：L3 缓存，也称为“Infinity Cache”。这两个 Radeon™ GPU 的 L3 缓存大小分别为 128 MB 和 96 MB，都足以容纳大小为 nx,ny = 1024,1024 的多个 xy 平面。从现在开始，对于 Radeon™ GPU，我们使用 LLC 来指代 L3 缓存，对于 Instinct™ GPU，我们使用 L2。

让我们快速进行一项新的扩展研究，以验证这两个 Radeon™ GPU 的 LLC 是否确实是较大尺寸下的性能限制因素。为确保我们不会耗尽内存，让我们从 nx,ny,nz = 1024,1024,32 开始，并缓慢增加 ny 的值。

图 4：在 RX 6900 XT 和 RX 7900 XTX GPU 上，增加 nx*ny 步幅对性能的影响

在上图中，当 xy 平面超过特定阈值时，有效内存带宽仍然会下降。当 xy 平面超过 32 MB 时，RX 6900 XT 性能下降；当 xy 平面超过 25 MB 时，RX 7900 XTX 性能下降。RX 7900 XTX 的 LLC 比 RX 6900 XT 小，因此性能在较小的 xy 平面尺寸下开始下降。无论使用哪种 AMD GPU，如果 nx * ny 过大，性能都会下降。

解决缓存大小限制

那么，我们如何解决这些更大问题上的缓存大小问题呢？这对于 MI50 这样的硬件尤其重要，因为其 LLC 仅为 4 MB L2 缓存。即使 nz 很小，但 nx 和 ny 值很大，L2 缓存也可能成为内存流量瓶颈。让我们考虑在 MI250X GCD 上进行下一个实验，当 nx,ny,nz = 1024,1024,1024 时。以下是解决 L2 缓存瓶颈的两种可能策略：

选项 1：网格块配置

如前所述，当前的线程块和网格索引配置按 x、y 和 z 方向提取元素。对于 nx,ny,nz = 1024,1024,1024 这样的大问题，这种方法会完全填充 L2 缓存，然后才能获取任何 z 方向的模板。让我们首先修改基线线程块配置 256 $\times$ 1 $\times$ 1，将其更改为 128 $\times$ 1 $\times$ 8。这需要我们将启动边界重置为默认值 1024，但让我们看看这个简单的更改是否会对性能产生任何影响。

性能有了显著提升——FOM 提高了 68%，提取效率接近 80%，L2 缓存命中率提高到 60% 以上。通过修改线程块配置以包含 z 方向的元素，HIP 内核在这些较大的问题规模上取得了显着的性能提升。然而，提取效率仍有约 20% 的提升空间。

另一个可以尝试的修改是仍然使用原始的 256 $\times$ 1 $\times$ 1，但配置 HIP 内核的网格启动和内核内的索引。这需要在主机端和设备端进行代码修改。对于主机端，我们修改网格启动配置：

dim3 grid(
    (nx - 1) / block.x + 1,
    (ny - 1) / (block.y * m) + 1,
    (nz - 1) / block.z + 1);

dim3 grid(
    (ny - 1) / (block.y * m) + 1,
    (nz - 1) / block.z + 1,
    (nx - 1) / block.x + 1);

第二个更改涉及配置 HIP 内核内的索引：

int i = threadIdx.x + blockIdx.x * blockDim.x;
int j = m*(threadIdx.y + blockIdx.y * blockDim.y);
int k = threadIdx.z + blockIdx.z * blockDim.z;

int i = threadIdx.x + blockIdx.z * blockDim.x;
int j = m*(threadIdx.y + blockIdx.x * blockDim.y);
int k = threadIdx.z + blockIdx.y * blockDim.z;

以前，blockIdx.x 和 blockIdx.y 索引分别在 x 和 y 方向上跨越 pos，加载大小为 nx * ny 的 xy 平面到缓存。现在，它们分别在 y 和 z 方向上跨越 pos，加载大小为 blockDim.x * ny 的 xy 平面到缓存。索引顺序的重新排列使多个 xy 平面的较小部分能够填充 L2 缓存，从而增加了其他线程块已获取的所有数据被有效重用的可能性。以下是性能数据：

这个修改后的网格索引实际上比之前修改线程块大小的性能更好。提取效率非常接近理论极限，L2 缓存命中率略有提高。然而，这种解决方法并不完美——最后一个示例是以 blockDim.x = 256 运行的，因此每个子 xy 平面占用大约 2 MB 内存，从而仍然允许三个不同的子 xy 平面适合 L2 缓存。较大的 nx * ny 平面将不可避免地面临与之前相同的问题。

选项 2：划分为子域

另一种更稳健地规避问题的方法是将整体问题规模划分为较小的域，以便三个 xy 平面能够适合 L2 缓存并串行化内核启动。当前的 xy 平面大小 nx,ny = 1024,1024 是之前考虑的、已知可以三次适合 L2 缓存的 xy 平面大小 nx,ny = 512,512 的 4 倍，因此我们考虑将其划分为 4 个子域。

让我们从回到 Kernel 5 开始。首先，我们修改主机端代码：

dim3 grid(
    (nx - 1) / block.x + 1,
    (ny - 1) / (block.y * m) + 1 ,
    (nz - 1) / block.z + 1);

...


laplacian_kernel<<<grid, block>>>(d_f, d_u, nx, ny, nz,
    invhx2, invhy2, invhz2, invhxyz2);

int bny = (ny - 1) / 4 + 1;
dim3 grid(
    (nx - 1) / block.x + 1,
    (bny - 1) / (block.y * m) + 1 ,
    (nz - 1) / block.z + 1);

...

for (int i = 0; i < 4; i++)
  laplacian_kernel<<<grid, block>>>(d_f, d_u, nx, ny, nz,
      invhx2, invhy2, invhz2, invhxyz2, bny*i);

代码中进行了三处更改。首先，我们将 grid.y 值修改为使用 bny = (ny - 1) / 4 + 1 而不是 ny，表明我们只在 y 方向上迭代四分之一的域。接下来，我们添加了一个 for 循环来启动四个 HIP 内核，以计算每个子域中的模板。最后，我们通过添加一个 y 方向偏移量来修改内核参数。设备内核需要修改如下：

__global__ void laplacian_kernel(T * f,
    const T * u, int nx, int ny, int nz,
    T invhx2, T invhy2, T invhz2, T invhxyz2) {

...

int j = m*(threadIdx.y + blockIdx.y * blockDim.y);

__global__ void laplacian_kernel(T * f,
    const T * u, int nx, int ny, int nz,
    T invhx2, T invhy2, T invhz2, T invhxyz2, int sy) {

...

int j = sy + m*(threadIdx.y + blockIdx.y * blockDim.y);

内核内的其他所有内容都可以保持不变。我们检查下面的性能：

FOM 比以前更高。提取效率也接近 100%，表明我们已经优化了内存移动。与以前的解决方法不同，这种方法对于处理任何大小的 xy 平面都是稳健的——xy 平面越大，用户可以划分成更多的子域。这种方法特别有用，如果您的内核将在 Radeon™ 和 Instinct™ GPU 上运行，因为不同的 LLC 大小会严重影响性能的“截止”点。虽然我们选择在 y 方向上划分问题大小，但也可以轻松地将此优化应用于 x 方向。

总结和回顾

在本部分中，我们首先检查了 Kernel 5 在各种 AMD GPU 和问题规模下的性能，并注意到当网格跨越特定尺寸阈值时，性能似乎会出现急剧下降。通过实验确定，LLC 的大小是大型 xy 平面问题性能的限制因素。提出了两种不同的解决方法来规避缓存大小问题，这两种方法都只需要修改几行代码。

在整个有限差分法拉普拉斯算子系列中，我们从一个简单的 HIP 内核实现开始，并逐步应用了几种不同的优化，以显着提高内核的性能。我们现在将快速回顾本工作中进行的所有不同优化：

1. 循环分块（第 2 部分）：如果已知内核加载多个可重用值，请考虑添加循环分块（也称为循环展开）。重构代码需要几个步骤，但这最终减少了启动的线程块数量并增加了每个线程计算的模板数量。使用这种方法可以大大减少 FETCH_SIZE。

2. 重排访问模式（第 2 部分）：频繁地通过向前和向后访问内存地址中的设备元素可能会过早地将可重用数据从缓存中逐出。内核应将所有加载指令重新排序为以单个方向访问数据，即按升序地址访问内存。为了正确利用循环分块优化，需要此优化。

3. 启动边界（第 3 部分）：如果内核的寄存器使用率非常高，应用启动边界可以使编译器在寄存器分配方面做出更明智的决策，从而改善寄存器压力。默认值为 1024 个线程，但我们强烈建议将其设置为内核将使用的线程数。

4. 非临时加载（第 3 部分）：输出数组 f 的元素不被任何其他线程或内核共享，因此内置函数允许有限差分模板计算以更高的缓存逐出优先级写回设备内存，从而为输入数组 u 释放更多缓存。

5. 网格块配置（第 4 部分）：绕过 L2 缓存溢出问题的快速方法是配置线程块或网格索引配置。这允许 xy 平面的较小段首先填充缓存，从而使某些线程可以在无需多次从全局内存中提取的情况下执行计算。

6. 划分为子域（第 4 部分）：如果整个问题受到 LLC 大小的限制，请考虑将问题划分为多个子域，并顺序启动 HIP 内核来处理每个子域。此方法非常稳健，可以根据需要针对任何 LLC 或问题大小进行定制。

结构化网格上的拉普拉斯算子的有限差分模板在 HIP 中相对容易实现。在未来的 Lab Notes 文章中，我们将考虑其他偏微分方程，例如声波方程，它将需要比这里显示的更高阶的模板。这很可能需要这些最后四篇文章中未概述的优化策略。尽管如此，我们相信应利用此拉普拉斯算子系列中概述的所有优化策略来充分发挥模板内核的性能。

配套代码示例

如果您有任何问题或评论，请在 GitHub 讨论区 与我们联系

[1]

测试使用 ROCm 5.3.0-63 版本进行。基准测试结果不是经过验证的性能数据，仅用于展示代码修改的相对性能改进。实际性能结果取决于多种因素，包括系统配置和环境设置，不保证结果的可重现性。