矩阵乘法是线性代数中的一个基本方面,并且是高性能计算(HPC)应用程序中无处不在的计算。自 AMD CDNA 架构推出以来,通用矩阵乘法 (GEMM) 计算现已通过矩阵核心处理单元得到硬件加速。矩阵核心加速的 GEMM 内核是 rocBLAS 等 BLAS 库的核心,但开发者也可以直接对其进行编程。受 GEMM 计算吞吐量限制的应用程序可以通过利用矩阵核心获得额外的加速。
AMD 的矩阵核心技术支持各种混合精度运算,使我们能够处理大型模型并为任何人工智能和机器学习工作负载组合提高内存密集型运算的性能。各种数值格式在不同应用中有其用途。例如,使用 8 位整数 (INT8) 进行 ML 推理,使用 32 位浮点数 (FP32) 数据进行 ML 训练和 HPC 应用,使用 16 位浮点数 (FP16) 数据进行图形工作负载,以及使用 16 位脑浮点数 (BF16) 数据进行 ML 训练,并减少收敛问题。
要详细了解与 SIMD 向量单元相比使用矩阵核心可实现的理论加速,请参阅下表。这些表列出了上一代 (MI100) 和当前一代 (MI250X) CDNA 加速器的向量(即融合乘加或 FMA)和矩阵核心单元的性能。
MI100 和 MI250X 的矩阵核心性能
| 数据格式 | MI100 Flops/Clock/CU | MI250X Flops/Clock/CU |
|---|---|---|
| FP64 | 不适用 | 256 |
| FP32 | 256 | 256 |
| FP16 | 1024 | 1024 |
| BF16 | 512 | 1024 |
| INT8 | 1024 | 1024 |
MI100 和 MI250X 的向量 (FMA) 单元性能
| 数据格式 | MI100 Flops/Clock/CU | MI250X Flops/Clock/CU |
|---|---|---|
| FP64 | 64 | 128 |
| FP32 | 128 | 128 |
MI100 和 MI250X 的矩阵核心与向量单元性能的加速比。注意,MI250X 还支持打包 FP32 指令,这使 FP32 吞吐量加倍
| 数据格式 | MI100 矩阵/向量加速比 | MI250X 矩阵/向量加速比 |
|---|---|---|
| FP64 | 不适用 | 2x |
| FP32 | 2x | 2x |
使用 AMD 矩阵核心
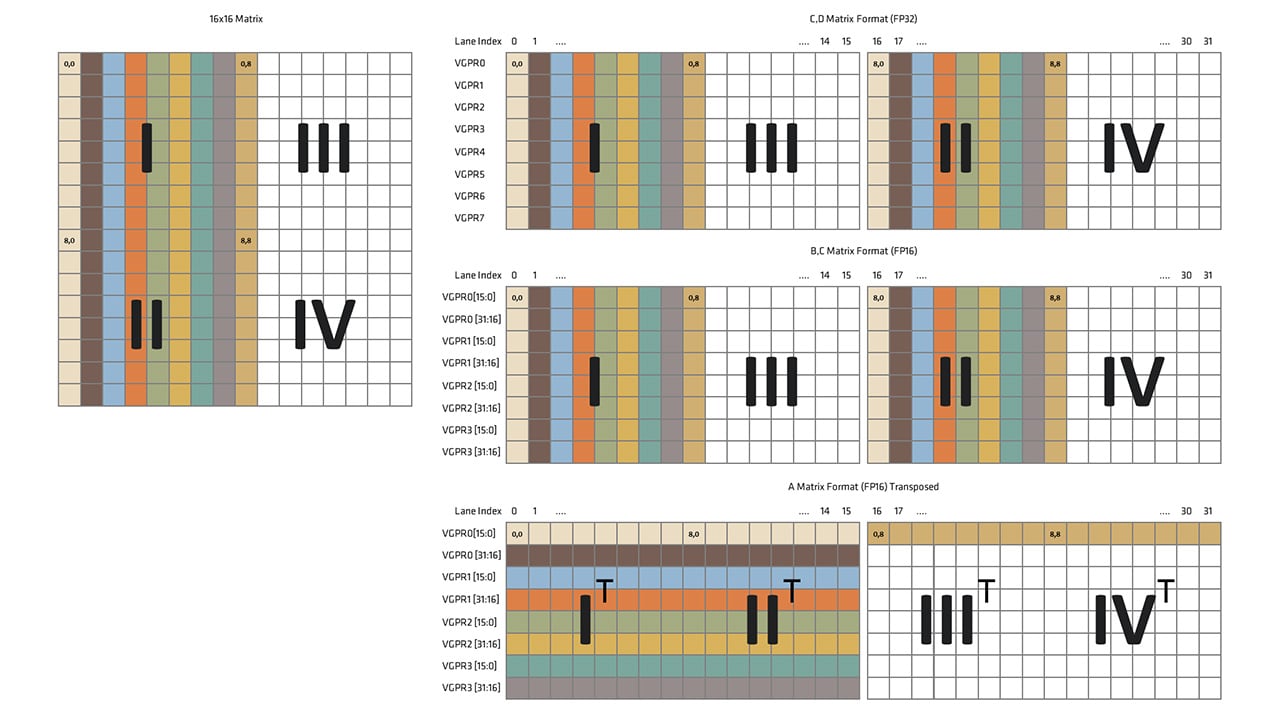
AMD CDNA GPU 中的矩阵融合乘加 (MFMA) 指令是基于波前 (wavefront) 而非单个通道 (lane/thread) 的:输入和输出矩阵的元素分布在波前向量寄存器的通道上。
AMD 矩阵核心可以通过多种方式利用。从高层来看,可以使用 rocBLAS 或 rocWMMA 等库在 GPU 上执行矩阵运算。例如,如果 MFMA 指令对当前计算有利,rocBLAS 可能会选择使用它们。对于更底层的操作,您可以选择
-
完全用汇编语言编写 GPU 内核(这可能有些挑战且不切实际)
-
在 HIP 内核中嵌入内联汇编(不推荐,因为编译器不会考虑内联指令的语义,并且可能不会处理数据依赖,例如在使用 MFMA 指令的结果之前必须等待的指定周期数)
-
使用编译器内在函数:这些函数代表汇编指令,以便编译器能够理解其语义和要求。
本文中的编码示例使用了一些可用的 MFMA 指令的编译器内在函数,并展示了如何将输入和输出矩阵的元素映射到波前向量寄存器的通道。所有示例都使用单个波前来计算小尺寸的矩阵乘法。这些示例并非旨在展示如何从 MFMA 操作中获得高吞吐量。
MFMA 编译器内在函数语法
考虑以下 MFMA 乘法运算,其中所有操作数 、、 和 均为矩阵:
要在 AMD GPU 上执行 MFMA 操作,LLVM 提供了内置的内在函数。请注意,这些内在函数是在整个波前上执行的,并且输入和输出矩阵的片段被加载到波前每个通道的寄存器中。MFMA 编译器内在函数的语法如下所示。
d = __builtin_amdgcn_mfma_CDFmt_MxNxKABFmt (a, b, c, cbsz, abid, blgp)
其中,
-
CDfmt是 和 矩阵的数据格式 -
ABfmt是 和 矩阵的数据格式 -
M、N和K是矩阵的维度-
mA[M][K]源 矩阵 -
mB[K][N]源 矩阵 -
mC[M][N]累加输入矩阵 -
mD[M][N]累加结果矩阵
-
-
a是存储来自源矩阵 的值的向量寄存器集合 -
b是存储来自源矩阵 的值的向量寄存器集合 -
c是存储来自累加输入矩阵 的值的向量寄存器集合 -
d是存储累加结果矩阵 的值的向量寄存器集合 -
cbsz(控制广播大小修饰符)用于更改输入值被馈送到矩阵核心的方式,并且仅支持具有多个输入块的 矩阵的指令。设置cbsz会告知指令将一个选定输入块的值广播到 中的 个相邻块。用于广播的输入块由abid参数确定。默认值 0 表示不进行值广播。例如,对于一个 16 块的 矩阵,设置cbsz=1将导致块 0 和 1 接收相同的值,块 2 和 3 接收相同的值,块 4 和 5 接收相同的值,依此类推。 -
abid(A 矩阵广播标识符)支持具有多个输入块的 矩阵的指令。它与cbsz一起使用,并指示选择哪个输入块以广播到 矩阵中的其他相邻块。例如,对于一个 16 块的 矩阵,设置cbsz=2和abid=1将导致块 1 的值被广播到块 0-3,块 5 的值被广播到块 4-7,块 9 的值被广播到块 8-11,依此类推。 -
blgp(B 矩阵通道组模式修饰符)允许对 矩阵数据在通道之间进行一组受限的混洗操作。对于支持此修饰符的指令,支持以下值:-
blgp=0的正常矩阵布局 -
blgp=1通道 0-31 的 矩阵数据也广播到通道 32-63 -
blgp=2通道 32-63 的 矩阵数据广播到通道 0-31 -
blgp=3矩阵数据从所有通道向下旋转 16(例如,通道 0 的数据放入通道 48,通道 16 的数据放入通道 0) -
blgp=4通道 0-15 的 矩阵数据广播到通道 16-31、32-47 和 48-63 -
blgp=5通道 16-31 的 矩阵数据广播到通道 0-15、32-47 和 48-63 -
blgp=6通道 32-47 的 矩阵数据广播到通道 0-15、16-31 和 48-63 -
blgp=7通道 48-63 的 矩阵数据广播到通道 0-15、16-31 和 32-47
-
CDNA2 GPU 支持的矩阵维度和块数如下表所示。
| A/B 数据格式 | C/D 数据格式 | M | N | K | 块 | 周期 | Flops/周期/CU |
|---|---|---|---|---|---|---|---|
| FP32 | FP32 | ||||||
| 32 | 32 | 2 | 1 | 64 | 256 | ||
| 32 | 32 | 1 | 2 | 64 | 256 | ||
| 16 | 16 | 4 | 1 | 32 | 256 | ||
| 16 | 16 | 1 | 4 | 32 | 256 | ||
| 4 | 4 | 1 | 16 | 8 | 256 | ||
| FP16 | FP32 | ||||||
| 32 | 32 | 8 | 1 | 64 | 1024 | ||
| 32 | 32 | 4 | 2 | 64 | 1024 | ||
| 16 | 16 | 16 | 1 | 32 | 1024 | ||
| 16 | 16 | 4 | 4 | 32 | 1024 | ||
| 4 | 4 | 4 | 16 | 8 | 1024 | ||
| INT8 | INT32 | ||||||
| 32 | 32 | 8 | 1 | 64 | 1024 | ||
| 32 | 32 | 4 | 2 | 64 | 1024 | ||
| 16 | 16 | 16 | 1 | 32 | 1024 | ||
| 16 | 16 | 4 | 4 | 32 | 1024 | ||
| 4 | 4 | 4 | 16 | 8 | 1024 | ||
| BF16 | FP32 | ||||||
| 32 | 32 | 8 | 1 | 64 | 1024 | ||
| 32 | 32 | 4 | 2 | 64 | 1024 | ||
| 16 | 16 | 16 | 1 | 32 | 1024 | ||
| 16 | 16 | 4 | 4 | 32 | 1024 | ||
| 4 | 4 | 4 | 16 | 8 | 1024 | ||
| 32 | 32 | 4 | 1 | 64 | 512 | ||
| 32 | 32 | 2 | 2 | 64 | 512 | ||
| 16 | 16 | 8 | 1 | 32 | 512 | ||
| 16 | 16 | 2 | 4 | 32 | 512 | ||
| 4 | 4 | 2 | 16 | 8 | 512 | ||
| FP64 | FP64 | ||||||
| 16 | 16 | 4 | 1 | 32 | 256 | ||
| 4 | 4 | 4 | 4 | 16 | 128 |
所有 CDNA2 架构支持的指令的完整列表可以在 AMD Instinct MI200 指令集架构参考指南 中找到。AMD 的 矩阵指令计算器 工具可以生成更多信息,例如 AMD Radeon™ 和 AMD Instinct™ 加速器上 MFMA 指令的计算吞吐量和寄存器使用情况。
示例 1 – V_MFMA_F32_16x16x4F32
考虑矩阵乘法运算 ,其中 且 ,元素类型为 FP32。假设输入 矩阵为了简化起见包含零。我们将演示如何使用内在函数 __builtin_amdgcn_mfma_f32_16x16x4f32,该函数在一词调用中计算四个外积的和。此函数作用于单个矩阵块。
输入矩阵 和 的维度分别为 和 ,而矩阵 和 包含 个元素,因此每个线程有 4 个元素需要存储,如图和代码片段所示。
以下两图显示 1) 和 输入的形状和大小;以及 2) 和 的元素如何映射到波前拥有的寄存器中的通道。
以下两图显示 1)输出矩阵 的形状和大小;以及 2) 的元素如何映射到波前拥有的寄存器中的通道。
执行此 MFMA 操作的内核示例如下。
#define M 16#define N 16#define K 4
__global__ void sgemm_16x16x4(const float *A, const float *B, float *D){ using float4 = __attribute__( (__vector_size__(K * sizeof(float)) )) float; float4 dmn = {0};
int mk = threadIdx.y + K * threadIdx.x; int kn = threadIdx.x + N * threadIdx.y;
float amk = A[mk]; float bkn = B[kn]; dmn = __builtin_amdgcn_mfma_f32_16x16x4f32(amk, bkn, dmn, 0, 0, 0);
for (int i = 0; i < 4; ++i) { const int idx = threadIdx.x + i * N + threadIdx.y * 4 * N; D[idx] = dmn[i]; }}此内核的启动方式如下。
dim3 grid (1, 1, 1);dim3 block(16, 4, 1);
sgemm_16x16x4 <<< grid, block >>> (d_A, d_B, d_D);如前所述,输入 矩阵假定包含零。
示例 2 – V_MFMA_F32_16x16x1F32
考虑矩阵乘法的场景,其维度为 和 ,使用编译器内建函数 __builtin_amdgcn_mfma_f32_16x16x1f32。在这种情况下,输入值可以仅由 wavefront 的 16 个车道持有。事实上,此指令可以同时乘以 4 个此类矩阵,从而使每个车道持有这 4 个矩阵之一的值。
我们可以重用上一示例中的图来说明此操作的数据布局。在此情况下,输入 不是一个 矩阵,而是四个 矩阵。但它们的布局方式,以及 wavefront 中每个车道拥有的元素是相同的。“列” 是独立的 矩阵。输入 类似。
给定矩阵乘法的输出具有与上一示例完全相同的数据布局。区别在于现在有四个独立的输出,每个输出对应一次乘法。
下面的内核展示了一个示例,用于对大小为 和 的 4 个打包矩阵的批量乘法。
#define M 16#define N 16#define K 1
__global__ void sgemm_16x16x1(const float *A, const float *B, float *D){ using float16 = __attribute__( (__vector_size__(16 * sizeof(float)) )) float; float16 dmnl = {0};
int mkl = K * threadIdx.x + M * K * threadIdx.y; int knl = threadIdx.x + N * K * threadIdx.y;
float amkl = A[mkl]; float bknl = B[knl];
dmnl = __builtin_amdgcn_mfma_f32_16x16x1f32(amkl, bknl, dnml, 0, 0, 0);
for (int l = 0; l < 4; ++l) { for (int i = 0; i < 4; ++i) { const int idx = threadIdx.x + i * N + threadIdx.y * 4 * N + l * M * N; D[idx] = dmnl[i]; } }}该内核是通过以下方式启动的:
dim3 grid (1, 1, 1);dim3 block(16, 4, 1);
sgemm_16x16x1 <<< grid, block >>> (d_A, d_B, d_D);示例 3 – V_MFMA_F64_4x4x4F64
考虑 V_MFMA_F64_4x4x4F64 指令,它计算四个独立矩阵块的 MFMA,大小为 。执行的操作为 ,其中 , , 和 都是大小为 的矩阵,且 。
下面的两张图显示了 1)输入参数 和 的四个分量的尺寸和形状,以及 2)这些分量如何映射到 wavefront 所拥有的寄存器中的车道。此指令的参数包括 、 、 并返回 ,因此我们知道每个参数和输出都包含 4 个矩阵。
输出 和输入 的布局与输入 的布局相同。
关于 rocWMMA 的说明
我们只展示了三个利用 AMD Matrix Core 通过编译器内建函数进行运算的示例。更多示例可以在这里找到。请注意,内建函数在未来可能会发生变化,因此最好使用 AMD 的 rocWMMA C++ 库来加速混合精度 MFMA 操作。rocWMMA API 能够将矩阵乘累加问题分解为片段,并在跨 wavefront 并行分布的块状操作中使用它们。该 API 是一个 GPU 设备代码的头库,允许矩阵核心加速直接编译到您的内核设备代码中。这可以受益于编译器在生成内核汇编方面的优化。更多详细信息请参阅 rocWMMA 仓库。
关于 AMD Matrix Instruction Calculator 工具的说明
对于那些想了解各种 MFMA 指令在 AMD Radeon™ 和 AMD Instinct™ 加速器上的性能,并希望了解矩阵元素与硬件寄存器之间映射关系的人,我们推荐 AMD Matrix Instruction Calculator 工具。这个强大的工具可以用来描述 WMMA 指令和给定架构的 MFMA ISA 级指令。我们欢迎社区 提交问题 和反馈。
参考文献
如果您有任何问题或评论,请在 GitHub 讨论区 与我们联系